Tag: reward

Categories
Forex Daily Topic Forex Risk Management

Position Size Risk and System Analysis

Introduction
Some authors label this topic as Money Management or Risk Management, but this misses the point. Money Management doesn’t tell much about what it does, and Risk Management seems

Introduction
Some authors label this topic as Money Management or Risk Management, but this misses the point. Money Management doesn’t tell much about what it does, and Risk Management seems

Introduction

Some authors label this topic as Money Management or Risk Management, but this misses the point. Money Management doesn’t tell much about what it does, and Risk Management seems more related to risk, which has been discussed on the subject of cutting losses short and let profits run.

However, Van K. Tharp has hit the point: He calls it position sizing, and it tells us how much to trade on every trade and how this is related to our goal settings and objectives.

1.    Risk and R

In his well-known book Trade your Way to your Financial Freedom, Van K. Tharp says that a key principle to success in trading is that the investor should always know his initial risk before entering a position.

He suggests that this risk should be normalized, and he calls it R. Your profits must also be normalized to a multiple of R, our initial risk.

The risk on one unit is a direct calculation of the difference in points, ticks, pips, or cents from the entry point to the stop-loss multiplied by the value of the minimum allowed lot or pip.

Consider, for example, the risk of a micro-lot of the EUR/USD pair in the following short entry:

        Size of a micro-lot: 1,000 units
                Entry point: 1.19344
                  Stop loss: 1.19621
Entry to stop-loss distance: 0.00277

Dollar Risk for one micro-lot: 0.00277 * 1,000 = $ 2.77
In this case, if the trader had set his $R risk – the amount he intends to risk on a trade – to be $100, what should be his position size?

Position size: $100/$2.77= -36 micro-lots (it’s a short trade)

Using this concept, we can standardize our position size according to the particular risk. For instance, if the unit risk in the previous example were $5 instead, the position size would be:

$100/5 = 20 micro-lots.

We would enter a position with a standard and controlled risk independent of the distance from entry to stop.

2.    Profit targets as multiples of R

Our profits can be normalized as multiples of the initial risk R. It doesn’t matter if we change our dollar risk from $100 to $150. If you keep our records using R multiples, you’ll get a normalized track record of your system.

With enough results, you’ll be able to understand how your system performs and, also, able to measure its statistical characteristics and its quality.

Values such as Expectancy (E), mean reward to risk ratio(RR), % of gainers, the number of R gains a system delivers (R multiple) in a day, week, month or year.

Knowing these numbers is very critical because it will help us to achieve our objectives.

You already know what Expectancy (E) is. But the beauty of this number is that, together with the average number of trades, it tells you the R multiple your system delivers in a time interval.

For example, let’s say you’ve got a system that takes six trades a day, and its E is 0.45R. This means it makes $0.45 per dollar risked.

 That means that the system also delivers an average of 0.45×6R=2.7R per day and that, on average, you’d expect, monthly, 54R.

Let’s say you wanted to use this system, and your monthly goal is  $6,000. What would your risk per trade be?

To answer this, you need to equate 54R = $6000

So your risk per trade should be set to:

R= 6000/60 = $111.

Now you know, for instance, that you could achieve $12,000/month by doubling our risk to $222 per trade and $24,000 if you can raise your risk to $444 per trade. You have converted a system into an exponential money-making machine, but with a risk-controlled attitude.

3.    Variability of the results 

As traders, we would like to know, also, what to expect from the system concerning drawdowns.

Is it normal to have 6, 10, 15, or 20 consecutive losses? And, what are the chances of a string of them to happen? Is your system misbehaving, or is it on track?
That can be answered, too, using the % of losers (PL).

Let’s consider, as an example, that we have a system with 50% winners and losers.

We know that the probability of an event A and an event B happening together is the probability of A happening times the probability of B happening:

ProbAB = ProbA * ProbB

For a string of losses, we have to multiply the probability of a loss by itself the number of times the streak duration.

So for a n streak:

Prob_Streak_n = PL to the power of n = PLn

As an example, the probability of 2 consecutive losses for the system of our example is:

Prob_Streak_2 = 0.52
= 0.25 or 25%

And the probability of suffering 4 consecutive losses will be:

Prob_Streak_4 = 0.54
= 0.0625 or 6.25%

For a string of six losses is:

Prob_Streak_6 = 0.56
= 0.015625, or 1.5625% 

And so on.

This result is in direct relation to the probability of ruin. If your R is such that a string of six losses wipes 100% of your capital, there is a probability of 1.56% for that to happen under this system.

Now we learned that we must set our dollar risk R to an amount such that a string of losses doesn’t bring the account beyond the maximum percent drawdown that is tolerable to the trader.

What happens if the system has 40% winners and 60% losers, as is usual on reward/risk systems? Let’s see:

Prob_Streak_2 = 0.62 = 36%

Prob_Streak_4 = 0.64 = 12.96%

Prob_Streak:6 = 0.66 = 4,66%

Prob_Streak_8 = 0.68 = 1.68% 

We observe that the probability of consecutive streaks of the same magnitude increases, so now the likelihood of eight straight losses in this system has the same probability as six in the former one.

This means that with systems with a lower percentage of winners, we should be more careful and reduce our maximum risk compared to a system with higher winning ratios.

As an example, let’s do an exercise to compute the maximum dollar risk for this system on a $10,000 account and a maximum tolerable drawdown of 30%. And assuming we wanted to withstand eight consecutive losses (a 1.68% probability of it to happen, but with a 100% probability of that to occur throughout a trader’s life).

According to this, we will assume a streak of eight consecutive losses, or 8R.

30% of $10,000 is $3,000

then 8R = $3,000, and

max R allowed is: 3000/8 = $375 or 3.75% of the account balance.

As a final caveat, to get an accurate enough measure of the percentage of losers, we should have more than 100 samples on our system history (forward tested, if possible, since back-tests usually presents unrealistic results). With just 30 points, the data is not representative enough to get any fair result.

You could do the same computations for winning streaks, using the percent of winners instead, and multiplying by the average reward (R multiple).

1.    Key points and conclusions

  • Position sizing is the part of the system that tells us how much to risk on a trade and is directly relevant to fulfilling our goals
  • The unit of risk R is a normalized symbol for dollar risk
  • You should measure, register, and be aware of the main statistical parameters of your systems: Expectancy, Percent winners and losers, reward to risk ratio, and the mean monthly-R (the average number of R your system achieves in one month)
  • You should compute the maximum R allowed by your system and account size for the max drawdown bearable for you, and not bet more than that amount.

©Forex.Academy

Categories
Forex Daily Topic Forex Price Action

Reversal Breakouts Offer a Lot

The trend is traders’ friend. Breakout is traders’ best friend. In today’s lesson, we are going to demonstrate an example of an H1 breakout, which makes a reversal even in the daily chart. Thus, the price heads towards the breakout direction with good momentum ending up offering an excellent reward. Let us get started.

The trend is traders’ friend. Breakout is traders’ best friend. In today’s lesson, we are going to demonstrate an example of an H1 breakout, which makes a reversal even in the daily chart. Thus, the price heads towards the breakout direction with good momentum ending up offering an excellent reward. Let us get started.

The trend is traders’ friend. Breakout is traders’ best friend. In today’s lesson, we are going to demonstrate an example of an H1 breakout, which makes a reversal even in the daily chart. Thus, the price heads towards the breakout direction with good momentum ending up offering an excellent reward. Let us get started.

The chart shows that the price makes a strong bearish move and finds its support. Upon producing a bullish engulfing candle, the price heads towards the North at a moderate pace. The price does not make a breakout at the last swing high. Thus, the chart is still bearish biased. Please note, the H1 chart does not show, but the daily trend has been bearish in this chart.

The chart shows that one of the candles breaches through the last swing high, closing well above the level. The last candle comes out as a bullish candle as well. It confirms the breakout. The buyers may wait for the price to consolidate and get a bullish reversal candle to go long in the pair.

The last two candles come out as bearish candles. The spinning top closes within the level of support. If the level produces a bullish engulfing candle, the buyers may go long in the pair.

The last candle comes out as a bullish engulfing candle closing well above consolidation resistance. The buyers may trigger a long entry right after the candle closes by setting stop loss below the level of support and by setting take profit with 1R.

The price heads towards the North with extreme bullish momentum. The way the chart looks, it seems it may continue its journey for a while. The chart shows that the buyers achieve their target within the next two candles after triggering the entry. Let us proceed to the following chart to see what the price does.

The last candle comes out as a bearish engulfing candle. It is produced at the second rejection as well. This means the chart forms a double top here. A double top resistance forming a bearish engulfing candle suggests that the price may make a bearish move here. However, if we calculate the length of the bullish move, it ends up being a very good one. This is what usually happens when the price makes a breakout at the last daily candle’s highest high when the daily chart is bearish and if the breakout takes place at the lowest low when the daily trend is bullish. Make sure the price consolidates and produces a strong reversal candle at the breakout level. If that happens, it often ends up offering an excellent reward in the end.

Categories
Crypto Daily Topic Forex Price Action

Calculate Risk-Reward along with Candle’s Attributes

In today’s lesson, we are going to demonstrate an example of the importance of risk-reward. To be successful in price action trading, traders are to calculate risk-reward before every single entry they execute. Let us find out from the charts below the importance of risk-reward.

In today’s lesson, we are going to demonstrate an example of the importance of risk-reward. To be successful in price action trading, traders are to calculate risk-reward before every single entry they execute. Let us find out from the charts below the importance of risk-reward.

In today’s lesson, we are going to demonstrate an example of the importance of risk-reward. To be successful in price action trading, traders are to calculate risk-reward before every single entry they execute. Let us find out from the charts below the importance of risk-reward.

The price heads towards the South with an average bearish momentum. Ideally, it is the sellers’ territory. However, it has come a long way. The buyers must wait for a strong bullish reversal candle to go long on this chart.

This is an extremely strong bullish reversal candle. The buyers may wait for the price to consolidate and produce a bullish reversal candle. Within a candle, things are very different now.

The chart produces a bearish inside bar. Thus, buyers may get more optimistic. They are to wait for a bullish engulfing candle closing above the last swing high to trigger a long entry. The price may travel towards the drawn level, which is a significant level of resistance on the chart.

The chart produces a bullish engulfing candle closing well above the last resistance. As explained earlier, the buyers are to set their stop loss below the last candle and trigger a short entry right after the candle closes. The question is whether they shall take a long entry here or not. Think about it. The last candle closes within the level of resistance. Technically, there is no space for the price for traveling towards the North unless it makes another breakout here. The reward is zero here.

As anticipated, the price consolidates again and struggles to make another breakout. The last candle comes out as a bearish candle. Thus, things do not look good for the buyers. It may change its direction. If it makes a bullish breakout, that is another ball game, though. Let us proceed to the next chart.

The price does not make a bullish breakout but changes its trend. It is the sellers’ territory again. By looking at the last candle, the sellers may trigger a short entry by setting their take profit at the last swing low.

In this lesson, we have seen that the trend-initiating candle and the signal candle both get 10 on 10. However, the chart does not offer an entry because there is no space for the price for traveling towards the upside. Consequently, the sellers take over and drive the price towards the downside. To sum up, we not only look at the candle’s attributes but also calculate risk-reward.

Categories
Forex Basics Forex Daily Topic

The Babe Ruth Syndrome

In his book More than you know, Michael J. Mauboussin tells the story of a portfolio manager working in an investment company of roughly twenty additional managers. After assessing the

In his book More than you know, Michael J. Mauboussin tells the story of a portfolio manager working in an investment company of roughly twenty additional managers. After assessing the

In his book More than you know, Michael J. Mauboussin tells the story of a portfolio manager working in an investment company of roughly twenty additional managers. After assessing the poor performance of the group, the company’s treasurer decided to evaluate each manager’s decision methods. So he measured how many of the assets under each manager outperformed the market, as he thought that a simple dart-throwing choice would produce 50% outperformers. This portfolio manager was in a shocking position because he was one of the best performers of the group while keeping the worst percent of outperforming stocks.

When asked why was such a discrepancy between his excellent results and his bad average of outperformers, he answered with a beautiful lesson in probability: The frequency of correctness does not matter; it is the magnitude of correctness that matters. 

Transposed to the trading profession, The frequency of the winners does not matter. What matters is the reward-to-risk ratio of the winners.

Expected-Value A bull Versus Bear Case.

Since a combination of both parameters will produce our results, how should we evaluate a trade situation?

Mauboussin recalls an anecdote taken from Nassim Taleb’s Fooled by Randomness, where Nassim was asked about his views of the markets. He said there was a 70% chance the market had a slight upward movement in the coming week. Someone noted that he was short on a significant position in S&P futures. That was the opposite of what he was telling was his view of the market. So, Taleb explained his position in the expected-value form:

Market events Probability Magnitude Expected Value
Market moves up 70% 1% 0.700%
Market moves down 30% -10% -3.000%
Total 100% -2.300%

  As we see, the most probable outcome is the market goes up, but the expected value of a long bet is negative, the reason being, their magnitude is asymmetric. 

Now, consider the change in perception about the market if we start trading using this kind of decision methodology. On the one hand, we would start looking at both sides of the market. The trader will use a more objective methodology, taking out most of the personal biases from the trading decision. On the other hand, trading will be more focused on the size of the reward than on the frequency of small ego satisfactions.

The use of a system based on the expected value of a move will have another useful side-effect. The system will be much less dependent on the frequency of success and more focused on the potential rewards for its risk.

We Assign to much value to the frequency of success

Consider the following equity graph:

 

Fig 1 – Game with 90% winners where the player pays 10 dollars on losers and gains 1 dollar on gainers

This is a simulation of a game with 90% winners but with a reward-to-risk ratio of 0.1. Which means a loss wipes the value of ten previous winners.

Then, consider the next equity graph:

Fig 1 – Game with 10% winners where the player pays 1 dollar on losers and gains 10 dollars on gainers

A couple of interesting conclusions from the above graphs. One is that being right is unimportant, and two, that we don’t need to predict to be profitable. What we need is a proper method to assess the odds, and most importantly, define the reward-to-risk situation of the trade, utilizing the Expected Value concept,

By focusing on rewards instead of frequency of gainers, our strategy is protected against a momentary drop in the percent of winners.

The profitability rule

P  > 1 / (1+ R)  [1]

The equation above that tells the minimum percent winners needed for a strategy to be profitable if its average reward-to-risk ratio is R.

Of course, using [1], we could solve the problem of the minimum reward-to-risk ratio R required for a system with percent winners P.

R > (1-P)/P    [2]

We can apply one of these formulas to a spreadsheet and get the following table, which shows the break-even points for reward-to-risk scenarios against the percent winners.

We can see that a high reward-to-risk factor is a terrific way to protect us against a losing streak. The higher the R, the better. Let’s suppose that R = 5xr where r is the risk. Under this scenario, we can be wrong four times for every winner and still be profitable.

Final words

It is tough to keep profitable a low reward-to-risk strategy because it is unlikely to maintain high rates of success over a long period.

If we can create strategies focused on reward-to-risk ratios beyond 2.5, forecasting is not an issue, as it only needs to be right more than 28.6% of the time.

We can build trading systems with Reward ratios as our main parameter, while the rest of them could just be considered improvements.

It is much more sound to build an analysis methodology that weighs both sides of the trade using the Expected value formula.

The real focus of a trader is to search and find low-risk opportunities, with low cost and high reward (showing positive Expected value).

 

Appendix: The Jupyter Notebook of the Game Simulator

%pylab inline
Populating the interactive namespace from numpy and matplotlib
%load_ext Cython
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
The Cython extension is already loaded. To reload it, use:
  %reload_ext Cython
from scipy import stats, integrate
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(color_codes=True)
import numpy as np
%%cython
import numpy as np
from matplotlib import pyplot as plt

# the computation of the account history. We use cython for faster results
# in the case of thousands of histories it matters.
# win: the amount gained per successful result , 
# Loss: the amount lost on failed results
# a game with reward to risk of 2 would result in win = 2, loss=1.
def pathplay(int nn, double win, double loss,double capital=100, double p=0.5):
    cdef double temp = capital
    a = np.random.binomial(1, p, nn)
    cdef int i=0
    rut=[]
    for n in a:
        if temp > capital/4: # definition of ruin as losing 75% of the initial capital.
            if n:
                temp = temp+win
            else:
                temp = temp-loss        
        rut.append(temp)
    return rut
# The main algorithm. 
arr= []
numpaths=1 # Nr of histories
mynn= 1000 # Number of trades/bets
capital = 1000 # Initial capital

# Creating the game path or paths in the case of several histories
for n in range(0,numpaths):
    pat =  pathplay(mynn, win= 1,loss =11, capital= cap, p = 90/100)
    arr.append(pat)

#Code to print the chart
with plt.style.context('seaborn-whitegrid'):
        fig, ax = plt.subplots(1, 1, figsize=(18, 10))
        plt.grid(b = True, which='major', color='0.6', linestyle='-')
        plt.xticks( color='k', size=30)
        plt.yticks( color='k', size=30)
        plt.ylabel('Account Balance ', fontsize=30)
        plt.xlabel('Trades', fontsize=30)
        line, = ax.plot([], [], lw=2)
        for pat in arr:
            plt.plot(range(0,mynn),pat)
        plt.show()

References:

More than you Know, Michael.J. Mauboussin

Fooled by randomness, Nassim. N. Taleb

 

 

Categories
Crypto Guides

How Does A Cryptocurrency Work? (Example – Bitcoin)

In the previous articles, we have learned the definition, properties, and purpose of cryptocurrency. But it is vital for us to know how cryptocurrencies work. In this article, let us

In the previous articles, we have learned the definition, properties, and purpose of cryptocurrency. But it is vital for us to know how cryptocurrencies work. In this article, let us

In the previous articles, we have learned the definition, properties, and purpose of cryptocurrency. But it is vital for us to know how cryptocurrencies work. In this article, let us find out that by taking the example of Bitcoin.

Below are some of the important terminologies you should know before going further.

Peer to Peer Network (P2P) – The networks where computational devices are joined together with the internet instead of using a central server are called peer to peer networks. Hence there is less chance of a network failure than the standard server model to form a network.

Miners – Miners are the participants in the network who validate transactions. Thus, the creation of new Bitcoins is often referred to as the mining of bitcoins.

Nodes – The individual computational devices in the network are called nodes. The nodes are joined to form a P2P network.

Consensus algorithms – To validate the transactions, the miners in the network should agree whether a transaction is valid or not. The blockchain network uses consensus algorithms to get this job done.

How does the Bitcoin network work?

The blockchain network is set up in a peer to peer way, enabling decentralization of the network effectively, removing the server model. Bitcoin network bundles a certain number of transactions into a block, and these blocks are linked using cryptographic hashing techniques. The miner should validate these blocks for the authenticity of the transactions. To confirm them, the system proposes a challenge to the miners, and the first miner to solve the problem, propagates the message throughout the network. The solution to the challenge is called ‘nonce.’ The complexity of finding this nonce increase as the number of blocks keeps increasing in the system. The other miners validate and approve the transactions if the transactions are not fraudulent.

Bitcoin as reward

The miner who achieves the solution first gets rewarded in the network in the form of Bitcoins. This is how and why the Bitcoins are generated in the network. The miners should be rewarded to keep them motivated and committed to the network. Without miners, the network wouldn’t be sustainable.

To transact Bitcoins in the network, users must pay transaction fees as well. These transaction fees are also in Bitcoin. Hence these transaction fees and Bitcoins generated are paid as a reward to the miners for validating the transactions.

POW as a consensus algorithm

Bitcoin uses Proof of Work (POW) as a consensus algorithm. POW proposes a challenge to the network, which is to be solved to validate the transactions. But why is it necessary? Because POW discourages denial of service. Below are the steps involved in POW in general.

  • The service requester requests service from the service provider.
  • The service provider gives a challenge that should be a bit complex for the service requester to resolve but easy enough for the service provider to check.
  • The service provider proposes this challenge to avoid the exploitation of the service from the service requester.

The exact same concept is used in the Bitcoin network, as well. The miner must expend a considerable amount of computational energy and electricity to solve the challenge. Because by doing this, he/she will not validate fraudulent transactions to be accurate. If they do validate fake transactions, they will lose all the time and computational power they spent and also the chance of gaining a reward. POW is the most efficient consensus algorithm so far, and it makes the Bitcoin network efficient.

We hope you understood the working of Bitcoin. Cryptocurrencies other than Bitcoin with different blockchains and consensus work in a different way. You will know about each of them in the upcoming articles. Let us know if you have any questions in the comments below. Cheers!

Categories
Forex Educational Library

The Trading Record

Introduction
Traders want to win. Nothing else matters to them; and they think and believe the most important question is timing the entry. Exits don’t matter at all, because if

Introduction
Traders want to win. Nothing else matters to them; and they think and believe the most important question is timing the entry. Exits don’t matter at all, because if

Introduction

Traders want to win. Nothing else matters to them; and they think and believe the most important question is timing the entry. Exits don’t matter at all, because if they time the entry, they could easily get out long before a retracement erases their profit. O so they believe.

That’s the reason there are thousands of books about Technical Analysis, Indicators, Elliott Wave Forecasting, and so on, and just a handful of books on psychology, statistical methods, and trading methodology.

The problem lies within us, not in the market. The truth is not out there. It is in here.

There are a lot of psychological problems that infest most of the traders. One of the most dangerous is the need to be right. They hate to lose, so they let their losses run hoping to cover at a market turn and cut their gains short, afraid to lose that small gain. This behavior, together with improper position sizing is the cause of failure in most of the traders.

The second one is the firm belief in the law of small numbers. This means the majority of unsuccessful traders infer long-term statistical properties based on very short-term data. When his trading system enters in a losing streak, they decide the system doesn’t work, so they look for another system which, again, is rejected when it enters in another losing sequence and so on.

There are two problems with this approach. The first one is that the trading account is constantly consumed because the trader is discarding the system when sits at its worst performance, adding negative bias to his performance every time he or she switches that way. The second one is that the wannabe trader cannot learn from the past nor he can improve it.

This article is a rough approach to the problem of establishing a trading methodology.

1.- Diversification

The first measure a trader should take is:

  1. A portfolio between 3-10 of uncorrelated and risk-adjusted assets; or
  2. A portfolio of 3 to 5 uncorrelated trading systems; or
  3. Both 1 and 2 working together.

What’s the advantage of a diversified portfolio:

The advantage of having a diversified portfolio of assets is that it smooths the equity curve and, and we get a substantial reduction in the total Drawdown. I’ve experienced myself the psychological advantage of having a large portfolio, especially if the volatility is high. Losing 10% on an asset is very hard, but if you have four winners at the same time, then that 10% is just a 2% loss in the overall account, that is compensated with, maybe, 4-6% profits on other securities. That, I can assure you, gave me the strength to follow my system!.

The advantage of three or more trading systems in tandem is twofold. It helps, also improving overall drawdown and smooth the equity curve, because we distribute the risk between the systems. It also helps to raise profits, since every system contributes to profits in good times, filling the hole the underperforming one is doing.

That doesn’t work all the time. There are days when all your assets tank, but overall a diversified portfolio together with a diversified catalog of strategies is a peacemaker for your soul.

2.- Trading Record

As we said, deciding that a Trading System has an edge isn’t a matter of evaluating the last five or ten trades. Even, evaluating the last 30 trades is not conclusive at all. And changing erratically from system to system is worse than random pick, for the reasons already discussed.

No system is perfect. At the same time, the market is dynamic. This week we may have a bull and low volatility market and next one, or next month, we are stuck in a high-volatility choppy market that threatens to deplet our account.

We, as traders need to adapt the system as much as is healthy. But we need to know what to adjust and by how much.

To gather information to make a proper analysis, we need to collect data. As much as possible. Thus, which kind of data do we need?

To answer this, we need to, first look at which kind of information do we really need. As traders, we would like to data about timing our entries, our exits, and our stop-loss levels. As for the entries we’d like to know if we are entering too early or too late. We’d like to know that also for the profit-taking. Finally, we’d like to optimize the distance between entry and stop loss.

To gather data to answer the timing questions and the stop loss optimum distance the data that we need to collect is:

  • Entry type (long or short)
  • Entry Date and time,
  • Entry Price
  • Planned Target price
  • Effective exit price
  • Exit date and time
  • Maximum Adverse Excursion (MAE)
  • Maximum Favourable Excursion(MFE)

All the above concepts are well known to most investors, except, maybe, the two bottom ones. So, let me focus this article a bit on them, since they are quite significant and useful, but not too well known.

MAE is the maximum adverse price movement against the direction of the trend before resuming a positive movement, excluding stops. I mean, We take stops out of this equation. We register the level at which a market turn to the side of our trade.

MFE is the maximum favourable price movement we get on a trade excluding targets. We register the maximum movement a trade delivers in our favour. We observe, also, that the red, losing trades don’t travel too much to the upside.

 

Having registered all these information, we can get the statistical evidence about how accurate our entry timing is, by analysing the average distance our profitable trades has to move in the red before moving to profitability.

If we pull the trigger too early, we will observe an increase in the magnitude of that mean distance together with a drop in the percent of gainers. If we enter too late, we may experience a very tiny average MAE but we are hurting our average MFE. Therefore, a tiny average MAE together with a lousy average MFE shows we need to reconsider earlier entries.

We can, then, set the invalidation level that defines our stop loss at a statistically significant level instead of at a level that is visible for any smart market participant. We should remember that the market is an adaptive creature. Our actions change it. It’s a typical case of the scientist influencing the results of the experiment by the mere fact of taking measurements.

Let’s have a look at a MAE graph of the same system after setting a proper stop loss:

Now All losing trades are mostly cut at 1.2% loss about the level we set as the optimum in our previous graph (Fig 2).  When this happens, we suffer a slight drop in the percent of gainers, but it should be tiny because most of the trades beyond MAE are losers. In this case, we went from 37.9% winners down to 37.08% but the Reward risk ratio of the system went from results 1.7 to 1.83, and the average trade went from $12.01 to $16.5.

In the same way, we could do an optimization analysis of our targets:

We observed that most of the trades were within a 2% excursion before dropping, so we set that target level. The result overall result was rather tiny. The Reward-to-risk ratio went to 1.84, and the average trade to 16.7

These are a few observations that help us fine-tune our system using the statistical properties of our trades, together with a visual inspection of the latest entries and exits in comparison with the actual price action.

Other statistical data can be extracted from the tracking record to assess the quality of the system and evaluate possible actions to correct its behaviour and assess essential trading parameters. Such as Maximum Drawdown of the system, which is very important to optimize our position size, or the trade statistics over time, which shows of the profitability of the system shrinks, stays stable or grows with time.

This kind of graph can be easily made on a spreadsheet. This case shows 12 years of trading history as I took it from a MACD trading system study as an example.

Of course, we could use the track record to compute derived and valuable information, to estimate the behaviour of the system under several position sizes, and calculate its weekly or monthly results based in the estimation, along with the different drawdown profiles shaped. Then, the trader could decide, based upon his personal tolerance for drawdown, which combination of Returns/drawdown fit his or her style and psychological tastes.

The point is, to get the information we must collect data. And we need information, a lot of it, to avoid falling into the “law of small numbers” fallacy, and also to optimize the system and our risk management.

Note: All images were produced using Multicharts 11 Trading Platform’s backtesting capabilities.

Categories
Forex Educational Library

Risk, Reward, and Profitability

The Nature of Risk and Opportunity
Trading literature is filled with vast amounts of information about market knowledge: fundamentals, Central Banks, events, economic developments and technical analysis. This information is

The Nature of Risk and Opportunity
Trading literature is filled with vast amounts of information about market knowledge: fundamentals, Central Banks, events, economic developments and technical analysis. This information is

The Nature of Risk and Opportunity

Trading literature is filled with vast amounts of information about market knowledge: fundamentals, Central Banks, events, economic developments and technical analysis. This information is believed necessary to provide the trader with the right information to improve their trading decisions.

On the other hand, the trader believes that success is linked to that knowledge and that a trade is good because the right piece of knowledge has been used, and a bad trade was wrong because the trader made a mistake or didn’t accurately analyse the trading set-up.

The focus in this kind of information leads most traders to think that entries are the most significant aspect of the trading profession, and they use most of their time to get “correct” entries. The other consequence is that novice traders prefer systems with high percent winners over other systems, without more in-depth analysis about other aspects.

The reality is that the market is characterized by its randomness; and that trading, as opposed to gambling, is not a closed game. Trading is open in its entry, length, and exit, which gives room for uncountable ways to define its rules. Therefore, the trader’s final equity is a combination of the probability of a positive outcome – frequency of success- and the outcome’s pay-off, or magnitude.

This latest variable, the reward-to-risk ratio of a system, technically called “the pay-off” but commonly called risk-reward ratio, is only marginally discussed in many trading books, but it deserves a closer in-depth study because it’s critical for the ultimate profitability of any trading system.

To help you see what I mean, Figure 1 shows a game with 10% percent winners that is highly profitable, because it holds a 20:1 risk-reward ratio.

A losing game is also possible to achieve with 90% winners:

So, as we see, just the percentage winners tell us nothing about a trading strategy. We need to specify both parameters to assess the ultimate behaviour of a system.

The equation of profitability

Let’s call Rr the mean risk-reward of a system.  If we call W the average winning trade and L the average losing trade then Rr is computed as follows:

Rr = W/L

If we call minimum P the percent winners needed to achieve profitability, then the equation that defines if a system is profitable in relation to a determined reward-risk ratio Rr is:

P > 1 / (1 +Rr) (1)

Starting from equation (1) we can also get the equation that defines the reward-risk needed to achieve profitability if we define percent winners P:

Rr > (1-P) / P (2)

If we use one of these formulas on a spreadsheet we will get a table like this one:

When we look at this table, we can see that, if the reward is 0.5, a trader would need two out of three winning trades just to break-even, while they would require only one winner every three trades in the case of a 2:1 payoff, and just one winner every four trades if the mean reward is three times its risk.

The lessons learned from analysing these equations are:

Let’s call nxR the opportunity of a trade, where R is the risk and n is the multiplier of R that defines the opportunity. Then we can observe that:

  1. If you spot an nxR opportunity, you could fail, on average, n-1 times and still be profitable.
  2. A higher nxR protects your account against a drop in the percent of gainers
  3. You don’t need to predict the price to make money because you can be profitable with 10% winners or less.
  4. As a corollary to 3, the real money comes from exits, not entries.
  5. The search for higher R-multiples with decent winning chances is the primary goal when designing a trading system.

A high Rr ratio is a kind of protection against a potential decline in the percentage of winning trades. Therefore, we should make sure our strategies acquire this kind of protection. Finally, we must avoid Rr’s under 1.0, since it requires higher than 50% winners, and that’s not easy to attain when we combine the usual entries with stop-loss protection.

One key idea by Dr. Van K. Tharp is the concept of the low-risk idea. As in business, in trading, a low-risk idea is a good opportunity with moderate cost and high reward, with a reasonable probability to succeed. By using this concept, we get rid of one of the main troubles of a trader: the belief that we need to predict the market to be successful.

As we stated in point 3 of lessons learned: we don’t need to predict. You’ll be perfectly well served with 20% winners if your risk reward is high enough. We just need to use our time to find low-risk opportunities with the proper risk-reward.

We can find a low-risk opportunity, just by price location as in figure 3. Here we employ of a triple bottom, inferred by three dojis, as a fair chance of a possible price turn, and we define our entry above the high of the latest doji, to let the market confirm our trade.  Rr is 3.71 from entry to target, so we need just one out of four similar opportunities for our strategy to be profitable.

Finally, we should use Rr as a way to filter out the trades of a system that don’t meet our criteria of what a low-risk trade is.

If, for instance, you’re using a moving average crossover as your trading strategy, by just filtering out the low profitable trades you will stop trading when price enters choppy channels.

Conclusions:

  • Risk-reward is the parameter that allows the assessment of the opportunity value of a trade.
  • The higher the opportunity, the less the frequency of winners we need to be profitable.
  • Therefore, we can assess an opportunity just by its intrinsic value, regardless of other factors.
  • That frees us from seeking accurate entries and set the focus on trade setup and follow-up.
  • We just need to use the familiar market concepts, for instance, support and resistance, to design a robust trading system, by filtering out all trades that don’t comply with the risk-reward figure.
  • Trading becomes the search for low-risk opportunities, instead of trying to forecast the market.

Appendix:

Example of Rr Calculation:

As we observe in Fig 3, the risk is defined by the distance between the entry price and the stop loss level, and the reward is the distance between the projected target level defined by the distance from the Take profit level to the entry price:

Risk = Entry price– Stop loss

Reward = Take profit – Entry price.

Rr = Reward / Risk

In this case,

Entry price  = 1.19355

Stop loss = 1.19259

Take profit = 1.19712

Therefore,

Risk = 1.19355 -1.19259 = 0.00096

Reward = 1.19712 – 1.19355 = 0.00357

Rr = 0.00357 / 0.00096

Rr = 3.7187

©Forex.Academy

Categories
Forex Educational Library

Trading, a Different Viewpoint: It’s all about Market Structure, Risk and System Design

Introduction
Globalization, the internet and also the massive use of computers have contributed to the worldwide spread of trading of all kinds: Stocks, futures, bonds, commodities, currencies. Even the weather

Introduction
Globalization, the internet and also the massive use of computers have contributed to the worldwide spread of trading of all kinds: Stocks, futures, bonds, commodities, currencies. Even the weather

Introduction

Globalization, the internet and also the massive use of computers have contributed to the worldwide spread of trading of all kinds: Stocks, futures, bonds, commodities, currencies. Even the weather forecast is traded!

In recent years, investors have turned their attention to the currency markets as a way to achieve their financial freedom. Forex is perceived as an easy place to achieve that goal. Trading currencies don’t know about bear markets. Currency pairs simply fluctuate driven by supply and demand in cycles of speculation-saturation, explained by behavioral economic science and game theory.

It looks straightforward: buy when a currency rises, sell once it falls.

However, this idyllic paradise has its own crocodiles that are required to be dealt with. The novel investor gets into this new territory armed with her own beliefs, that fitted well in his normal life but it’s utterly wrong when trading. But the main issues relating to underperformance lies inside the mind of the trader. Some say the market is rigged to fool most traders, however, the reality is that traders fool themselves. A shift in their core beliefs – and in the way they think-  is critical for them to succeed.

The purpose of this, divided into three parts, is to boost awareness concerning three main issues the trader faces:

  • The true knowledge about the nature of the trading environment
  • The nature of risk and opportunity
  • The key success factors when designing a system

The trading environment

Usually, people approach the study of the market environment by focusing mainly on market knowledge: Fundamentals, world news, central banks, meetings, interest rates, economic developments, etc. At that point, they interminably analyze currency technicalities: Overbought-oversold, trends, support-resistance, channels, moving averages, Fibonacci and so on.

They think that success is identified with that sort of information; that a trade has been positive because they were right on the market, and when it’s not is because they were wrong.

Huge amounts of paper and bytes have been spent in books and articles about those topics, yet there’s a concealed reality down there not yet uncovered, despite the fact that it’s the primary driver for the failure of the majority of traders (the other one is over-leverage and over-trading).

It’s evident that all traders are aware of the uncertainty of doing currency trading. Yet, except for individuals proficient about probability distributions, I am tempted to state that not a single person really knew what is this about, when she decided to trade currencies (at least not me, by the way).

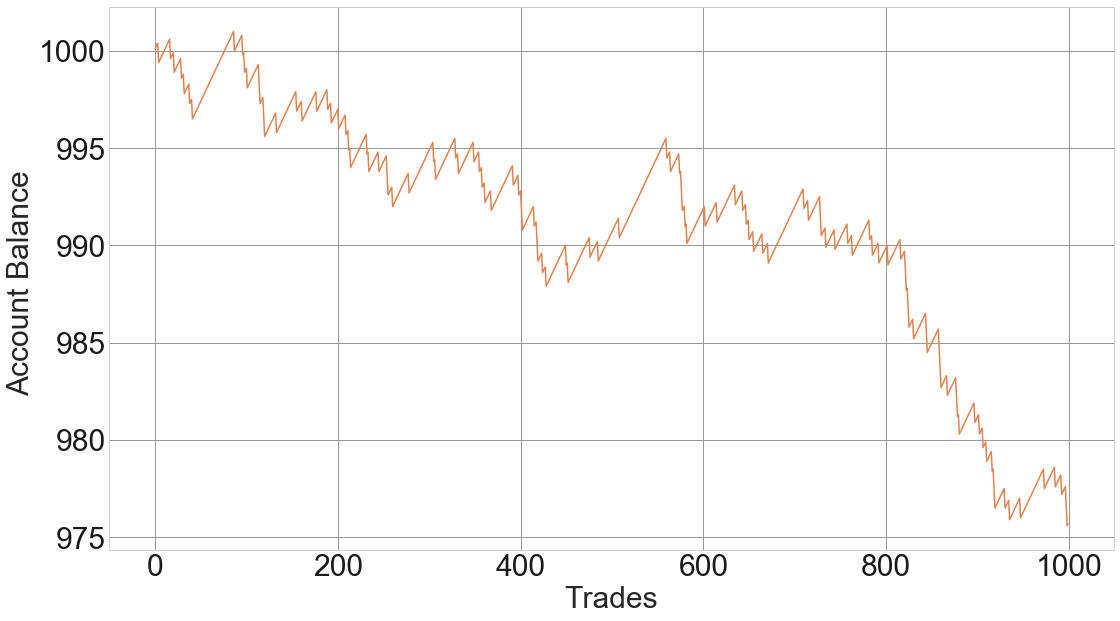
So, let’s begin. Everybody knows what a fair coin flip is, but what’s the balance of a fair coin flip game, starting 100€, after 100 flips if we earn 1€ when heads and lose 1€ when tails?

Many would say close to zero, and they might be right, but this is just one possible path:Fig 1: 100 flips of a fair coin flip game

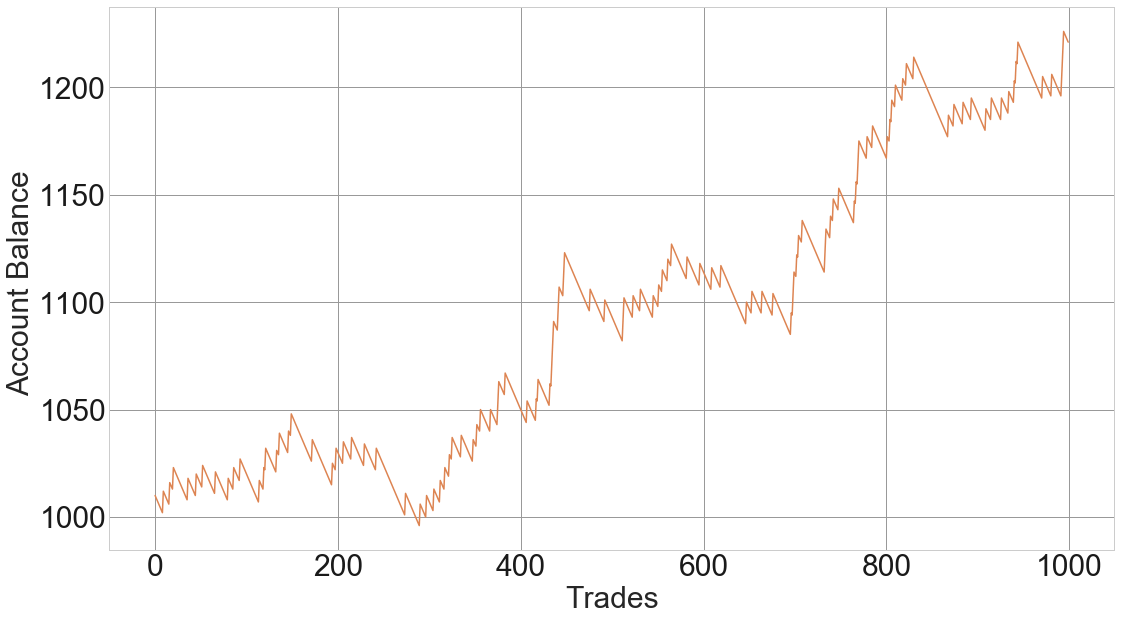
There are other paths, for instance, this one that loses more than 20€:

Fig 2: 100 different fair coin flips

This second path seems taken from a totally different game, but the nature of the random processes is baffling, and usually fools us into believing those two graphs are made from different games (distributions) although they’re not.

If we do a graph with 1,000 different games, we’d observe this kind of image:

Fig 3: 1,000 paths of a fair coin flip 100 flips long

Below, a flip coin with a small handicap against the gambler:

Fig 4: 1,000 paths of an unfair coin flip

Finally, a coin flip game with a slight advantage for the player:

Fig 5: 1,000 paths of a coin flip with edge

And that’s the genuine nature of the beast. This figure above corresponds to a diffusion process and each path is called random walk. Diffusion processes happen in nature, likewise, for instance, as a billow of smoke ascending out from a cigarette or the spread of a droplet of watercolor in a glass filled with clean water.

Our first observation regarding fig 4 is that the mean of the smoke cloud drifts with negative slope, so after the 100 games, just about 1/3 of them are above its initial value; and we may observe that, even in the fair coin case, 50% of paths end in negative territory.

The game of a coin flip with an edge (fig 5) is the only one that’s a winner long term, although, short-term, it might be a losing game. In fact, before the first 20 flips, close to 50% of them are underwater, and at flip Nr. 100 about 35% of all paths end losing money.

If that game were a trading system, it would be a fairly good one, with a mean profit of 70% after 500 trades, but how many traders would hold it after 50 trades? My figure: only a 30% lucky traders. The rest would drop it out; even that long-term performance is good enough.

Below fig 6 shows a diffusion graph of 1500 bets of that game, roughly the number of trades a system that takes six daily bets produces in a year. We see that absolutely all paths end positive and the mean total profit is about 200%.

Fig 6: 1,000 paths of a coin flip with edge

By the way, the edge in this game is just a reward to risk ratio of 1.3:1, while keeping a fair coin flip.

Before going into explaining the psychological aspects of what we’ve seen so far, let me show you some observations we’ve learned so far, regarding this phenomena:

  • The nature of the random environment fools the major part of the people
  • There are unlucky paths: Having an edge is no guarantee for a trader’s success (short term).
  • A casino game and the market, as well, collect money from endless hordes of gamblers with thin pockets and weak hands because they have no profitable system or stop trading his system before it could manifest its long-term edge.
  • Casino owners know the math of gambling and protect themselves against volatility by diversification and a maximum allowed bet (only small gamblers allowed).
  • By playing several uncorrelated paths at the same time, we could lower the overall risk, as does the casino owner, but we’d still need an edge and a proper psychological attitude.
  • A system without edge is always a loser, long term.

The psychology of decisions taken under uncertainty

In 2002, Daniel Kahneman received the Nobel prize in economics “for having integrated insights from psychological research into economic science, especially concerning human judgment and decision-making under uncertainty.”

Dr.Kahneman did most of this work with Dr. Amos Tversky, who died in 1966. Their studies opened a new field of economics: Behavioural finance. They called it Prospect Theory and dealt with how investors make decisions under uncertainty and how they choose between alternatives.

One of the behaviors studied was loss aversion. Loss aversion shows the tendency for traders to feel more pain when taking a loss than the joy they feel when taking a profit.

Loss aversion has its complementary conduct: fear of regret. Investors don’t like to make mistakes. Both mechanisms combined are responsible for their compulsion to cut gains short and let loses run.

Another conduct taken from Prospect theory is that individuals believe in the law of small numbers: The tendency of people to infer long-term behavior using a small set of samples. They suffer from myopic loss aversion by assigning excessive significance to short-term losses, abandoning a beneficial long-term strategy because of suboptimal short-term behavior.

That’s the reason people gamble or trade until an unlucky losing streak happens to them, and the main reason casinos and the markets profit from people. Those who lose early, exit because they had depleted their pockets or their patience. Lucky winners will bet until a losing streak wipes their gains.

To abstain from falling into those traps, we should develop a strategy and get the strength and discipline to follow it, instead of looking too closely at results.

In Decision Traps, Russo and Schoemaker, have an illustrative approach to point to the process vs. outcomes dilemma:

Fig 7: Russo and Schoemaker: Process vs Outcomes.

Results are important and they are more easily evaluated and quantified than processes, but traders make the mistake to presume that good results come from good processes and bad results came from bad ones. As we saw here, this may be false, so we should concentrate on making our framework as robust as possible and focus on following our rules.

– A good decision is to follow our rules, even if the result is a loss

– A bad decision is not following our rules, even if the result is a winner.

The Nature of risk and opportunity

To help us in the task of exploring and finding a good trading system we’ll examine the features of risk and opportunity.

We’ll define risk as the amount of money we are willing to lose in order to get a profit.  We may call it a cost instead of risk since it’s truly the cost of our operations. From now on, let’s call this cost R.

We define opportunity as a multiple of R. Of course, as good businesspeople, we expect that the opportunity is worth the risk, so we should value most those opportunities whose returns are higher than the risk involved. The higher, the better.

From the preceding section, we realize that the majority of new investors and traders tend to cut gains and let the losses run, in an attempt for their losses to turn into profits, caused by the need to be right. Therefore, they prefer a trading system that’s right most of the time to a system that’s wrong most of the time, without any other consideration.

The novel trader looks for ideas that could make their system right, endlessly back-testing and optimizing it. The issue is that its enhancements are focused in the wrong direction, and, likewise, most likely ending over-optimized. Thus, with almost certainty, the resulting system won’t perform well in practice on any aspect (expectancy, % gainers, R/r, robustness…)

The focus on probability is sound when the outcomes are symmetrical (Reward/risk =1); otherwise, we must take into account the size of the opportunity as well.

So, we’d like a frame of reference that helps us in our job.  That frame will be achieved using, again, the assistance of our beloved diffusion cloud. The two parameters we’ll toy with will be: percent of gainers and also the Reward to risk (or Opportunity to cost ratio).

Since the goal of this exercise is to expel the misconceptions of the typical trader, we’ll use an extreme example: A winning system that’s right just 10% of the time, however with an R/r =10. It isn’t too pretty. It’s simply to point out that percent gainers don’t matter much:

 Fig 8: A game with 10% winners, and R/r = 10.

Right! One 10xR winner overtakes nine losers.

The only downside employing a system with parameters like this is that there’s a 5% chance to experience 30 consecutive losses, something tough to swallow.

But there are five really bright ideas taken from this exercise:

  • If you find an nxR opportunity you could fail on average n-1 times out of n and, still be profitable. Therefore, you only need to be right just one out of n times on an nX reward to risk opportunity.
  • A higher nxR protects us against a drop in the percent of gainers of our system, making it more robust
  • You don’t need to predict price movement to make money
  • Repeat; You don’t need to predict prices to make money
  • If you don’t have to predict, then the real money comes from exits, not entries.
  • The search for higher R-multiples with decent winning chances is the primary goal when designing a trading system.

Below it’s a table with the break-even point winning rate against nxR

Fig 9: nxR vs. break-even point in % winners.

We should look at the reward ratio nxR as a kind of insurance against a potential drop in the percent of winners, and make sure our systems inherit that sort of safe protection. Finally, we must avoid nxR’s below 1.0, since it forces our system to percent winners higher than 50%, and that’s very difficult to attain combined with stop losses and normal trading indicators.

Now, I feel we all know far better what we should seek: Looking for what a good businessperson does: Good opportunities with reduced cost and a reasonable likelihood to happen.

That’s what Dr. Van K. Tharp calls Low-risk ideas. A low-risk idea may be found simply by price location compared to some recent high, low or long-term moving average. As an example, let’s see this chart:

Fig 10: EUR/USD 15 min chart.

Here we make use of a triple bottom, suggested by three dojis, as a sign that there is a possible price turn, and we define our trigger as the price above the high of the latest doji. The stochastics in over-sold condition and crossing the 20-line to the upside is the second sign in favor of the hypothesis. There has a 3.71R profit on the table from entry to target, so the opportunity is there for us to pick.

Here it is another example using a simple moving average 10-3 crossover, but taking only those signals with more than 2xR:

Fig 10b: USD/CAD 15 min chart. In green 2xR trades using MA x-overs. In red trades that don’t pass the 2xR condition

Those are simply examples. The main purpose is, there are lots of ideas on trading signals: support-resistance, MA crossovers, breakouts, MACD, Stochastics, channels, Candlestick patterns, double and triple tops and bottoms, ABC pattern etc. However, all those ought to be weighed against its R-multiple payoff before being taken. Another point to remember is that good exits and risk control are more important than entries.

Key success factors when designing a system

Yeo Keon Hee, in his book Peak Performance Forex Trading, defines the three most vital elements of successful trading:

  1. Establishing a well-defined trading system
  2. Developing a consistent way to control risk
  3. Having the discipline to respect all trading rules defined in point 1 and 2

Those three points are essential, however not unique. We need additional tasks to perfect our job and our results as traders:

  1. Using proper position sizing to help us achieve our objectives.
  2. Keeping a trading diary, with annotations of our feelings, beliefs, and errors, while trading.
  3. A trading record including position size, entry date, exit date, entry price, stop price, target price, exit price, the nxR planned, the nxR achieved; and optionally the max adverse excursion and max favorable excursion as well.
  4. A continuous improvement method: A systematic review task that periodically looks at our trading record and draws conclusions about our trading actions, errors, profit taking, stop placement etc. and apply corrections/improvements to the system.

First of all, let’s define what a system is:

Van K Tharp wrote an article [1] about the subject. There he stated that what most traders think is a trading system, he would call it a trading strategy.

To me, the major takeaway of Van K. Tharp’s view of what a system means is the idea that a system is some structure designed to accomplish some objectives. In reference to McDonald’s, as an example of a business system, he says “a system is something that is repeatable, simple enough to be run by a 16-year-old who might not be that bright, and works well enough to keep many people returning as customers”.

You can fully read this interesting article by clicking on the link [1]  at the bottom of this document. Therefore I won’t expand more on this subject. If I discussed it, it was owing to the appealing thought of a system, as some structure designed to accomplish some goals that work mechanically or managed by people with average intelligence.

In this section, we won’t discuss details concerning entries, stop losses and exits- that’s a subject for other articles- however. We’ll examine the statistical properties of a sound system, and we’ll compare them with those from a bad system, so we could learn something about the way to advance in our pursuit.

Let’s begin by saying that in order to make sure the parameters of our system are representative of the entire universe of possibilities, we’d need an ample sample of trades taken from all possible scenarios that the system may encounter. Professionals test their systems using a multiyear database (10+ years as a minimum); however, an absolute minimum of 100 trades is a must, though it’s beyond the lowest size I might accept.

The mathematics of profitability

The main key feature of a sound system isn’t the percentage of gainers, but expectancy E (the expected value of trades).

Expectancy is the expected value of winners (E+) less the expected value of losers (E-)

(E+) = Sum(G)/(n+)  x  %Winners

(E-) = Sum(L)/(n-)  x  %Losers

Sum(G): The total dollar gains in our sample history, excluding losers

Sum(L): The total dollar losses in our sample history, excluding winners

(n+): The number of positive trades(Gainers)

(n-): The number of negative trades(Losers)

The expectancy E then is:

E = (E+) – (E-)

Similarly, we can compute

E = SUM(trade results)/n

Where n = total number of trades,

So E is the normalized mean or total results divided by the number of trades n.

If E is positive the system is good. The higher the E is, the better the system is, as well. If E is zero or negative, the system is a loser, even though the percentage of gainers was over 80%.

Another measure of goodness is the variation of results. Dr. Chis Anderson (main consultant for Dr. Van K. Tharp on his book about position sizing) explains that, for him, expectancy E is a measure of the non-random (or edge) part of the trade, and that we are able to determine if that edge is real or not, statistically.

From the trade list, we can also calculate the standard deviation of the set (STD).

From the trade list, we can also calculate the standard deviation of the set (STD). That can be done in Excel or by some other statistical package (Python, R, etc.). This is a measure of the variability of those results around the mean(E).

A ratio of E divided by the STD is a good metric of how big our edge is, relative to random variations. This can be coupled quite directly to how smooth the equity curve is.

Dr. Van K Tharp uses this measure to compute what he calls the System Quality Number (SQN)

SQN = 100 x E / STDEV

Dr. Anderson says he’s happy if the STDEV is five times smaller than E, that systems with those kind of figures show drawdown characteristics he can live with. That means SQN >= 2 are excellent systems.

As an exercise about the way to progress from a lousy system up to a decent and quite usable one, let’s start by looking at the stats, and other interesting metrics, of a bad system- a real draft for a currencies system- and, next, tweak it to try improving its performance:

STATISTICS OF THE ORIGINAL SYSTEM: 

Nr. of trades             : 143.00
gainers                   : 58.74%
Profit Factor             : 1.06
Mean nxR                  : 0.74
sample stats parameters:      
mean(Expectancy)          : 0.0228
Standard dev              : 1.6351
VAN K THARP SQN           : 0.1396

Our sample is 143 long, with 58.74% winners, but the mean nxR is just 0.74, therefore the combination of those two parameters results in E = 0.0228, or just 2,28 cents per dollar risked. SQN at 0.1396 shows it’s unsuitable to trade.

Let’s see the histogram of losses:

Histogram of R-losers

Fig 11: Histogram of R-losers (normalized to R=1)

Original system probability of profits of x R-size

Histogram of R-Profits

Fig 12: Histogram of R-Profits (normalized to R=1)

Diffusion cloud of 10,000 synthetic histories of the system:

Original system: Diffusion cloud 10,000 histories of 1,000 trades

Fig 13: Original system: Diffusion cloud 10,000 histories of 1,000 trades.

Histogram of Expectancy of 10,000 synthetic histories:

Expectancy histogram of 10,000 histories of 1,000 trades

Fig 14: Expectancy histogram of 10,000 histories of 1,000 trades. 50% of them are negative

We notice that the main source of information about what to improve lies in the histograms of losses and profits. There, we may note that we need to trim losses as a first measure. Also, the histogram of profits shows that there are too many trades with just a tinny profit. We don’t know what causes all this: Entries taken too early; too soon, or too late, on exits, or a combination of these factors. Therefore, we must examine trade by trade to find out that information and make the needed changes.

As a theoretical exercise, let’s assume we did that and, as a consequence of these modifications, we’ve reduced losses bigger than 2R by half and, also improved profits below 0.5R by two. The rest of the losses and profits remain unchanged.  Let’s see the stats of the new system:

IMPROVED SYSTEM STATISTICS:  
Nr. of trades             : 143.00 %
gainers                   : 58.74%
Profit Factor             : 1.99
mean nxR                  : 1.40 

sample stats parameters:       
mean(Expectancy)          : 0.4081
Standard dev              : 2.2007  
VAN K THARP SQN           : 1.8546

By doing this we’ve achieved an expectancy of 41 cents per dollar risked and an SQN of 1.53. It isn’t a perfect system, but it’s already usable to trade, even better than the average system:

Improved system: Diffusion cloud 10,000 histories of 1,000 trades

Fig 15: Improved system: Diffusion cloud 10,000 histories of 1,000 trades.

We may notice, also, on the histogram of Expectancies, below, that, besides owning a higher mean, all values of the distribution lie in positive territory. That’s an excellent sign of robustness and a good edge.

Expectancy histogram of 10,000 histories of 1,000 trades

Fig 17: Improved system: Expectancy histogram of 10,000 histories of 1,000 trades.

There are other complementary data we can extract that reveal other aspects of the system, such those below:

Trading System: It’s All About Market Structure, Risk & System Design

Trading System

Fig 17, for instance, shows that the system has a 40% chance of having 2 winners in a row, and 15% chance of 3 of them. Also, from fig 18, there’s a 60% chance of 2 loses in a row, 37% chance of 3 losers and 5% chance of a streak of 7 losers, so we must prepare ourselves against this eventuality by proper risk management.

Throughout this exercise, we’ve learned how to use our past trading information to analyze a system, decide what parts need to be modified, then perform the modifications, continue by testing it again using a new batch of results and observe if the new statistical data is sufficiently good to approve it for trading. Otherwise, a new round of modifications must be carried out.

Position Sizing

All figures and stats we’ve seen until now belong to an R-normalized system: It trades just a unity of risk per trade, without any position sizing strategy at all. That is needed to characterize the system properly. But the real value of a framework that allows this type of measurements is to use it as a scenario planning to experiment with different position sizing strategies.

We should remember, a system is a structure to achieve specific goals.

And position size is the method that helps us to achieve the financial goal of that system, at a determined financial maximum risk.

As an exercise, Let’s look at what this system may accomplish by maximizing position size without regard for risk (besides not going broke).

We’ll do it using Ralf Vince’s optimal f: The optimal fraction of our running capital. The computation of optimal f for this system was done using a Python script over 10,000 synthetic histories and resulted in a mean Opt f = 22%. To be on the safe side, we’ll use 75% of this value. That means the system will bet 16.77% of the running capital on every trade.

The result of the diffusion cloud will be shown in semi-log scale to make it fit the graph:

Diffusion cloud traded with Optimal f. y log scale

Fig 19: Improved system: Diffusion cloud traded with Optimal f. y log scale.

Below the probability curve of the log of profits, on a starting 10,000€ account, after 1000 trades:Trading System curve

Starting capital   :  1.0 e+4
Mean ending Capital:  2.54013596e+10
Min  ending Capital:  4.20930083e+02
Max  ending Capital:  3.94680594e+18

We see that there is 50% chance that our capital ends at 25,400 million euro (2.54 e+10) after 1000 trades, and a small chance of that figure is 3+ digits higher. Of course, the market will stop delivering profits much early than this. The purpose of the exercise is to show the power of compounding using position sizing.

Let’s see the drawdown curve of this positioning strategy:

Curve of Trading System

We observe there’s 80% chance our max drawdown being more than 75% and 20% chance of it being 90%, so this kind of roller-coaster isn’t for the faint heart!

Before finishing with this scenario, let’s look at a final graph:

trading curve

This graph shows the probability to reach 10x our initial capital after n trades. For this system, we observe that there’s a 25% chance (one out of 4 paths) that we could reach 10X in less than 80 trades and a 50% chance this happens in less than 150 trades.

That shows an important property of the optimal f strategy: Optimal f is the fastest way to grow a portfolio. The closer we approach optimal f the faster it grows. But as position size goes beyond the optimal fraction the risk keeps increasing but the profit diminishes, so there’s no incentive to trade beyond that point.

That property may suggest ideas about an alternative use the use of optimal f. If you think about a bit, surely, you’ll find some of them.

My goal with this exercise was to show that any average system can achieve any desirable objective.

Now let’s do another useful exercise. Let’s compute the fraction that fulfills a given objective limited by a given drawdown.

Let’s do a position sizing strategy for the faint-heart trader. He doesn’t wish more than 10% drawdown, accepting a 5% probability that drawdown goes to 15%. His primary concern is the risk, so he takes what the system could deliver within that small risk.

To find this sweet spot we need to try several sizes on our simulator using different fractions until that spot is reached. After a couple of trials, we find that the right amount for this system is to trade 1% of the running balance on each trade. Here we assumed that no other systems are used, and just one trade at a time. If several positions are needed, then the portfolio should be divided, or, alternatively, we must compute the characteristics of all systems combined.

Below, the main figures of the resulting system:

Starting Capital   :  10,000 | forex academy

Starting Capital   :  10,000
Mean ending Capital:  45,508
Min  ending Capital:  13,406
Max  ending Capital:  177,833

Trading System - Forex Academy

Mean drawdown: 9.58%
Max drawdown: 25.98%
Min drawdown: 4.13%

We observe, the system performs quite well for such small drawdown, with 100% of all paths more than doubling the capital, and a mean return of 455% after 1,000 trades.

Trading System - Forex.Academy

Finally, the figures for a bold trader who is willing to risk 30% of its capital, with just a small chance of more than 40%, are shown below.

FA

Starting Capital   :  10,000
Mean ending Capital:  710,455
Min  ending Capital:  19,890
Max  ending Capital:  37,924,312

FOREX TRADING SYSTEM

Mean drawdown: 26.43%
Max drawdown: 60.52%
Min drawdown: 11.97%

We observe that this positioning size is about 2.5 times riskier than the previous one. In the more conservative position sizing, we have a 5% chance of 15% max drawdown, while this one has a 5% chance of about 38% drawdown. But on returns we go from a mean ending capital of 45,500€ to a mean ending capital of 710,455€, surpassing by more than 10 times the returns of the first strategy.

This is common in position sizing compounding. Drawdowns grow arithmetically, returns grow geometrically.

Summary

Throughout this document, we’ve learned quite a bit about the three main aspects of trading.

Let’s summarize:

Nature of the trading environment

  • The nature of the random environment fools a majority of the people
  • New traders want to be right so they cut their profits while hanging on their losses
  • New traders are psychologically affected by the law of small numbers, and fail because they believe in the law of small numbers instead of being confident by the long-term edge of their system.
  • Having an edge is no guarantee for a trader’s success (short term) of you don’t have an edge and the discipline to follow your system.
  • By splitting the risk into several uncorrelated paths at the same time, we could lower the overall risk
  • A system without edge is always a loser long term.

The nature of risk and opportunity

  • If we look for nxR opportunities, we just need to succeed once every n trades be profitable.
  • A system with higher nxR is protected against a drop in the percent of gainers of our system, making it more robust.
  • We don’t need to predict price movement to make money.
  • If we don’t need to predict, then real money comes from exits, not from entries.
  • The search for higher R-multiples with decent winning chances is the primary goal when designing a trading system.

Key factors to look when developing a system

  • A system is a structure designed to accomplish specific goals that work automatically.
  • The three most vital elements of successful trading:
    • Establishing a well-defined trading system
    • Developing a consistent way of controlling risk
    • Having the discipline to respect all trading rules defined in point 1 and 2
  • Using proper position sizing helps us achieve our objectives.
  • Keeping a trading diary, with annotations of our feelings, beliefs, and errors, while trading.
  • It’s essential to keep a trading record
  • We need a continuous improvement method: A systematic review task that periodically looks at our trading records and draws conclusions about our trading actions, errors, profit-taking, stop placement, etc. and apply corrections/improvements to the system.
  • Position sizing is the tool to help us achieve our specific objectives about profits and risk.

References

[1] http://www.stockbangladesh.com/blog/what-is-a-trading-system-by-van-k-tharp/

Recommended readings:

Trade your way to your financial freedom, Van K. Tharp

Peak performance Forex Trading, Yeo, Keong Hee

Categories
Forex Educational Library

The Meaning of Cutting Losses Short

Abstract
In this article, we deal with the different ways and aspects of the stop-loss setting. A crucial task for a successful trader.
Introduction
What a price to pay for

Abstract
In this article, we deal with the different ways and aspects of the stop-loss setting. A crucial task for a successful trader.
Introduction
What a price to pay for

Abstract

In this article, we deal with the different ways and aspects of the stop-loss setting. A crucial task for a successful trader.

Introduction

What a price to pay for bad wisdom? Too young to know too much too soon… (Suzanne Vega)

The decision where to cut losses if a trade is not working should be part of the trade selection process for every trade, and should be assessed in connection to the potential profit; so the risk to reward should comply with our trading rules.

One key example of the need for cutting losses short (in other words having high reward to risk trades) was given by trader Glen Ring when interviewed by Bruce Babcock (The Four Cardinal Principles of Trading).

He had a month when he made eight trades, with seven winners and one loser, but the net result was a losing month, just because of a single big loss.

The opposite may hold: you might experience eight trades with seven losers and still be profitable just because your system’s mean reward-to-risk ratio is excellent and that winning trade erased the losses of the seven losers.

The key lesson is: Although psychologically, we need to be right, we must focus on a reward-to-risk ratio, not in the frequency of our gains.

In Glen’s words: “Having those small losses is what keep us in the game, keeps your position for when you do catch a trend or big move. But, it’s a law of numbers to me. If we can make enough controlled-loss trades, even a blind squirrel is going to find a nut once in a while.”

The Stop-Loss Concept

The stop-loss concept is related to position size. Trend following’s main idea is to catch the big trend. Its rate of success is reduced -below 35%-, but with potential big reward to risk ratios.

There’s a small chance for a trader to have ten losses in a row. A trader that risk no more than 2% of its equity on a single trade experiences a 20% drawdown at the end of 10 consecutive losses, but may still keep following the rules. A trader risking 5-6% will be 50 or 60% down, and undoubtedly will lose perspective and may stop following the rules, even though the system hasn’t failed.
The main lesson is: Trade thin instead of big at the beginning, analyze your potential drawdowns in losing streaks as a mean to optimize your position size of your system.

Minimizing losses means that we are in control. Being in control is the difference between being a speculator and a gambler. Being a speculator means we can decide on the odds. Be in control about when to enter the market and when to exit. That can’t be done gambling.

We’ll discuss the several methods top traders use in their trading systems. They can be divided into the following categories:

  • Chart-based stops
  • Indicator stops
  • Entry method stops
  • Volatility stops
  • Money management stops
  • Account equity stops
  • Margin-based stops

 

1.    chart-based stops

Chart-based stops are those stops put near a meaningful point on a chart. This may be related to a chart pattern, trend line or pivot point that represents support or resistance.

Cutting losses short don’t mean unrealistic tight stops, though. It’s important to give latitude enough to let the trade work.

So, cutting losses short means to close a trade if, by our rules, has touched the stop point. But that point shall be placed according to the logic of the price movement.

Also, it’s wise to let a wide margin at the beginning of the trade using a small position, but, as the trade develops in our favor, we should move the stop higher and, optionally, add to the position.

What happens if the chart stop defines a trade that’s too risky? In the futures market, the minimum risk one can take is the one assumed by trading one contract. In the case of currency markets, this isn’t an issue, so the answer is: reduce your position to the level you have set in your trading rules. The number one rule is to protect our capital.

The chart method to set the stop has its detractors. In Babcock’s book already mentioned, Jake Bernstein says that John Granville used to say: “if it’s obvious, it’s obviously wrong.” “Let’s put the stop at the low of the day.” Ten thousand people are thinking the same way. The odds are that approach is not going to work.

How To Set Stop Loss In Options Trading

The Last Day Rule:

Peter Brandt, mentioned in Babcock’s book, has what he calls “the last day rule”. He applies it to breakout trades to reduce losses on failed breakouts.

The rule calls for a stop set at the opposite extreme of the last day of the previous range pattern. If the break is to the upside, he sets the stop to the low of the last day within the pattern. If to the downside, he uses the high of that last day.

The use of retracements, Fibonacci:

Some traders use retracements as places to start a trade using Fibonacci retracements. One way to place entries and stops is, for instance, entries at a 50% retracement and stops at 62%, that way we plan for a 50% potential profit with a 12% risk; more than 4:1 RR.

Moving to break-even:

One method that helps release stress and anxiety from the trader is to move the stop to the break-even point if and when the price has moved to a level that allows to do it.  Then the rest of the trade is a free ride. This has been recommended by many authors focused on trader’s psychology (Alexander Elder, Mark Douglas, Van K. Tharp).

2.    indicator stops

Indicator stop means setting the stop by virtue of an indicator, such as a moving average or momentum.  It’s not a chart-based stop since it’s computationally based.

Indicator stops seek to optimize the relationship between cutting losses short and not getting chopped up at the same time. That’s difficult to achieve without studying past trades for improvement. Indicator stops tries to optimize the relationship between cutting losses short and not getting chopped up at the same time. That’s difficult to achieve without studying past trades for improvement.

To optimize stops we need to back (or forward) test which is the stop distance beyond which there is are more money lost than gained. For more on this, I recommend John Sweeney’s concept of Maximum Adverse Execution. To optimize stops we need to back (or forward) test which is the stop distance beyond which there is are more money lost than gained. For more on this, I recommend John Sweeney’s concept of Maximum Adverse Execution.

The main idea of the MAE using Sweeney’s words is:

 “It turns out that if your trading rules are consistent and can distinguish between good and bad trades, then, over many experiences, you can measure how far good trades go bad and, usually, see at what point a trade is more likely to end badly than profitably. That is the point at which you stop and/or reverse.”

 

How To Set Stop Loss In Options Trading | Forex Academy

How To Set Stop Loss In trading

(figures taken from John Sweeney’s book)

3.    entry method stops

By entry method stops, it means some stop point that is set by the entry method. It may be a reverse entry signal, or it may occur as a result of the violation of some or all of the trade’s entry conditions.

“The same methodology that says enter the trade has to tell you when the trade is wrong. [..] If a market exceeds the price and time projection windows, then the trade is wrong” (Robert Miner)

Robert Miner has a price and time zone. If price breaks the zone or if the time window is reached without gains, he closes the position.

4.    volatility stops

Volatility stops are stops placed at a distance from the entry calculated as some percentage of recent or historical volatility. In general, volatility is measured as a price range computed over a time-lapse.

Stan Tamulevich, interviewed by Babcock for his book, uses the three to four-day volatility. If the market takes out the distance of the last day, he quits the trade. Usually even less than that. If the market takes out 50% of last day move ¡t enters in a danger zone.

Russell Wasendorf, another trader interviewed, sets his stop outside the range set by historical volatility. Short-term volatility increases don’t change his plan. His method is more concerned with not getting shaken off a potentially winning position rather than improve its short-term risk.

5.    money management stops

Money management stops mean fixed dollar amount stops. It’s a combination of stops and dollar risk management.

The two main advantages the author sees are:

  • If the purpose of stop-loss is to manage risk, a dollar stop is the most direct way to manage it.
  •  That kind of stops don’t go to obvious places, except by coincidence, so the risk to be whipsawed by the market is reduced.

6.    account equity stops

An Equity stop is based on a fixed percentage of the account equity. A variant of money management stop.

It’s a methodology that starts by defining in dollar terms what’s the risk allowed by the account’s rolling balance of the trader. If we assume 1% risk is set,  this leads to a dollar risk amount for that account balance.

Then the risk-dollar amount of the potential trade is computed. If it falls within the 1% risk the trade is taken, opening the number of contracts within the 1% risk rule.

If the loss is not within the 1% rule, the entry point must be adapted to bring it close enough to the exit point, so the risk is no more than 1%.

7.    margin-based stops

A variation of the previous type. Stops are calculated by taking a percentage of the exchange margin. This is specific to futures trading.

8.    main points to remember

  • Cutting losses short is the most important rule in a trading plan
  • The trader should be more concerned with the reward-to-risk ratios than with the percentage of winning trades.
  • Chart-based stops set stop points in the proximity of market bottoms/tops.
  • Indicator-based stops look to optimize the stop point using math and historical analysis of past trades.
  • Volatility stops try to keep stop points away from the volatility cloud.
  • Account-equity stops move the entry point of a trade to a place that complies with the percent risk rules of the account.

9.    conclusions and criticism

Stop-loss definition is a difficult task, but it has to be designed with care, as is the main concept to success in trading.

In Mr. Babcock’s book, the primary focus is the futures market, that presents a very poor atomization of the position. I mean, the minimum size allowed in the futures market is ONE contract so that the minimum risk would be the risk of that single contract from an entry point to a stop point. That makes it difficult to split the concept of “cutting losses” with the concept of “position size.” In the currency markets, this is not the case, as we can do it down to micro-lots, which makes it possible to do independent optimization of the two concepts.

I think a combination of Chart or volatility-based stops is the initial stage towards the definition of this task as part of a trading system. But a second step might be to optimize stops using John Sweeney’s MAE concept. For this, we might need a computerized analysis of our past trades, or a back-test, if the system rules can be automated.

We may design a continuous improvement process, by a careful annotation of the behavior of our current stops for further analysis in search of better places.

Regarding position sizing, this is a subject for another essay, it suffices to say for the moment that we could use the before mentioned rule: don’t to risk more than 1% of our current trading account balance, and if you’re starting trading, don’t risk more than 25% of that. There’s a Spanish popular wisdom sentence: ” En dinero y amistad, la mitad de la mitad” (about money and friendship divide by half and then by half).

We should remember that the primary goal of a trader is to survive.

 ©Forex.Academy