Position Sizing IX: Improving the Percent Risk Model-Playing with market’s money
One way to improve the returns of a position sizing strategy without increasing our capital risk is to play with the market’s money. In this video, we are going to develop this idea as a way to improve the percent-risk model.
The market’s money
We define as “market’s money” the gains resulting from the profits of previous trade or winning streak. This is a mentality shift. Instead of viewing recent profits as your own money, you momentarily consider them as a gift of the market to increase the trading size riskless. This has a slight resemblance to moving your stops to break even and let the trade go on. After that action, the rest of the trade evolution is riskless. The concept of the market’s money is especially attractive when the trading strategy has a high percentage of winners because high probability strategies show a higher likelihood of winning streak versus losing streaks.
There are several ways to use this concept, but in this video, we will focus our attention on its use with the Percent-risk model. Precisely, we will use the money gained in the previous successful trades to increase the size of the next trade without increasing the risk of our base money.
The N-Step up position Sizing Strategy
The N-Step-up method uses the N previous successful trades’ gains to increase the size of the next trade. After N trades, the profit is added to the general wallet, to start a new cycle. If there is a loss, the cycle resets and begins again.
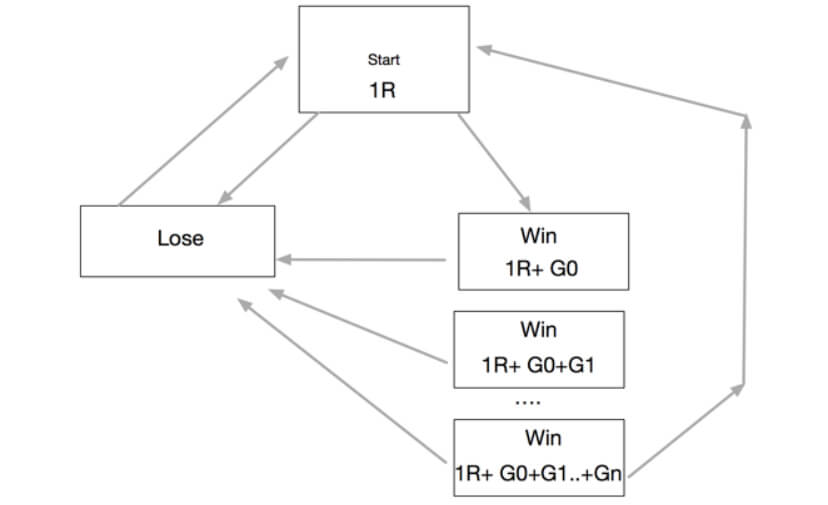
The flowchart of this methodology is shown below.
The key idea is that, even when it ends at a loss in the N step, the risk incurred is the only the risk made in the starting position, But if the N-cycle ends as a win, on a 1R reward/risk situation, it will end up with R+2R+3R+… NR gains. On a 2R reward/risk strategy, it will be 2R+6R+ 14R +…
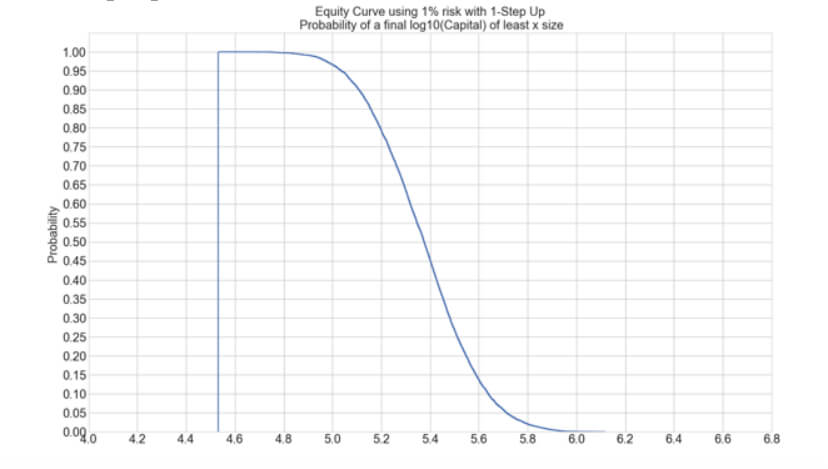
We will try this methodology using the Live Signals Service performance and 1% basic risk to see how the N-Step Up improves it.
Original 1% Strategy
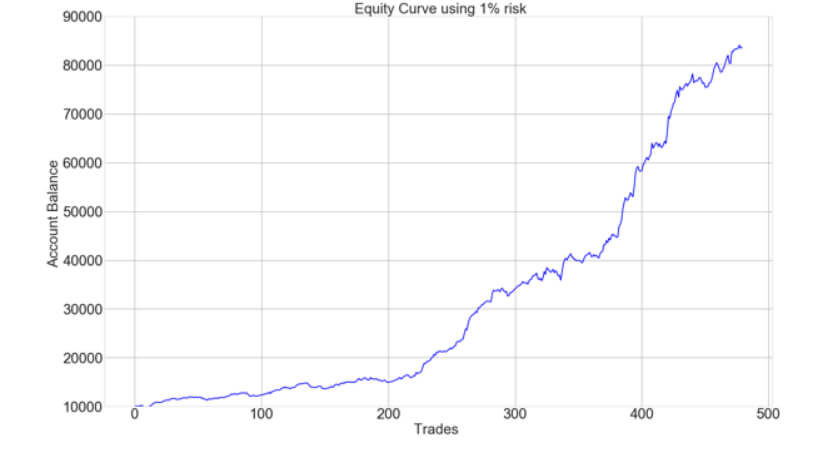
The graph below shows the equity curve growth using a 1% risk over one year of trading, assuming 2 daily trades on average.
When we use Monte Carlo resampling to get 10,000 different 1-year histories, we get the following information.
Average ending Capital: 75,359.86
Max ending Capital : 219,145.26
Min ending Capital: 26,811.62
Probability of Capital ending above 78,604: 43.98 %
Probability of Capital ending above 26,812: 99.99 %
Probability of Capital ending above 10,000: 100.00 %
In the figure below, we can see the likelihood of max drawdown for the 1% Risk model:
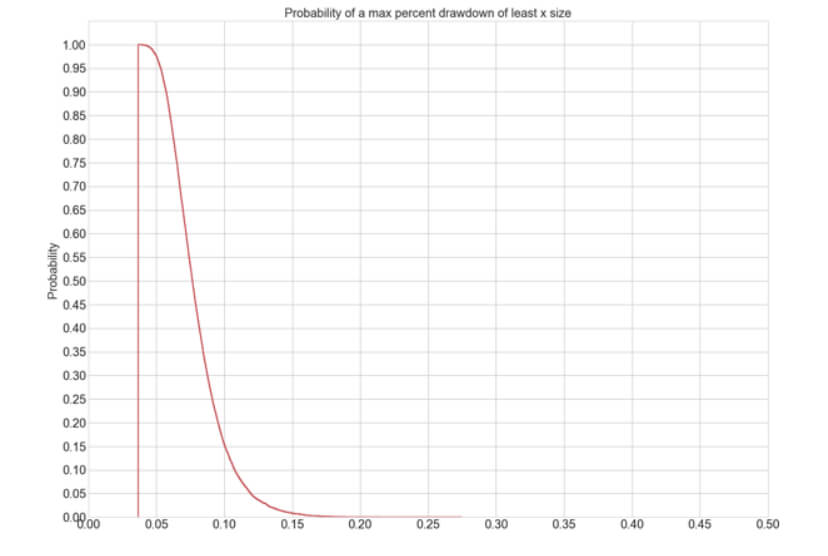
Average Max Drawdown: 8.02 %
Maximum Max Drawdown: 27.46 %
Min Max Drawdown: 3.67 %
Probability of a 10% drawdown: 15.44%
Probability of a 20& drawdown: 0.03%
Probability of a 30% drawdown: 0.00%
We can see that the expected max drawdown is 8.38%, with a one in five years ending at 10% and almost no chance to reach 20 percent. Let’s see how this can be improved with one, two, and three N-Step cycles.
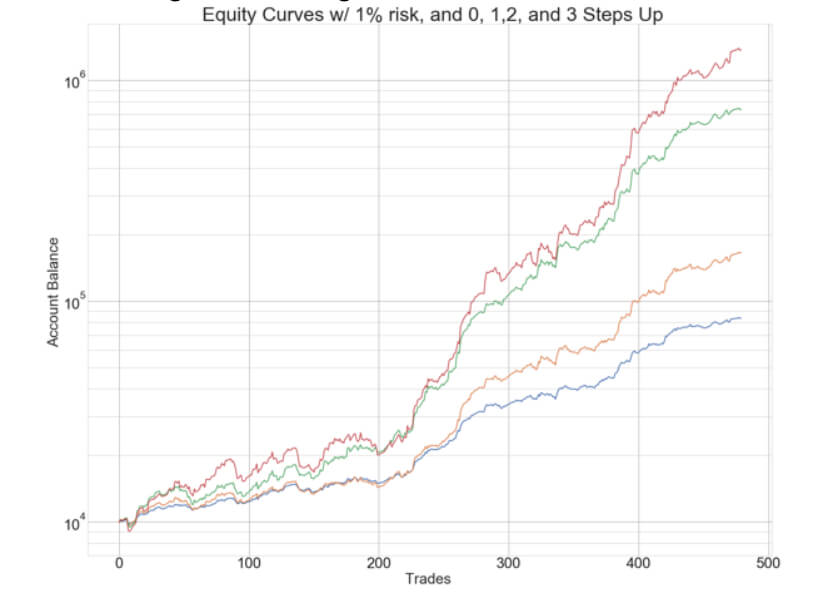
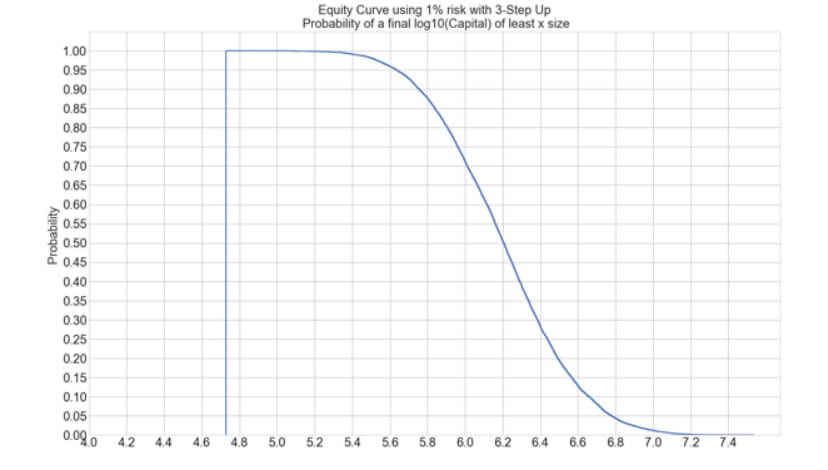
The below chart shows the original, plus 1-, 2- and 3-step up position sizing strategies, using semi-log scales to make them fit together in a single chart.
We can see that the advantage of using the methodology is evident, as the 3-Step-up sizing strategy reaches an ending capital of up to one order of magnitude higher (10X), as compared to the basic 1% Risk method.
Let’s see how they perform regarding returns and drawdowns:
1-Step Up Return Stats:
Average ending Capital: 236,427.55
Max ending Capital : 1,306,952.10
Min ending Capital: 34,015.66
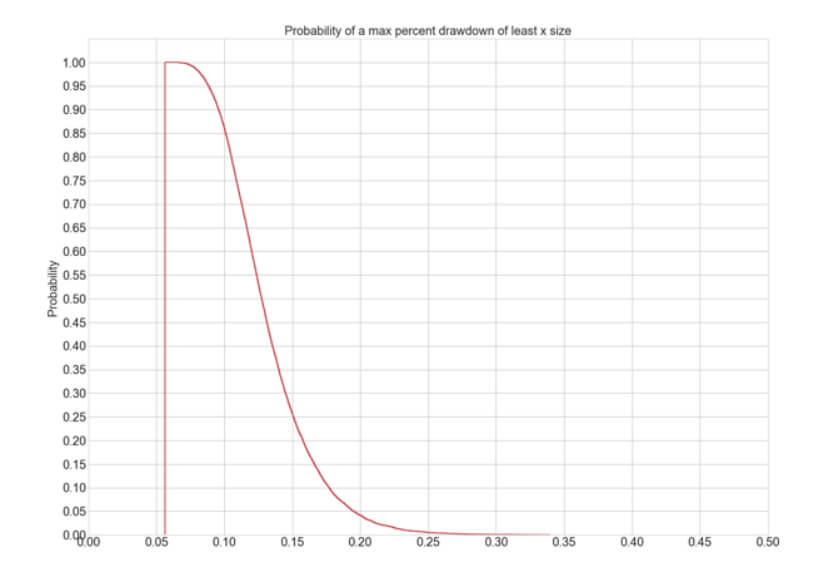
1-Step Up Drawdown figures:
Average Max Drawdown: 13.29 %
Maximum Max Drawdown: 33.94 %
Min Max Drawdown: 5.64 %
Probability of a 10% drawdown: 86.21%
Probability of a 20& drawdown: 4.15%
Probability of a 30% drawdown: 0.00%
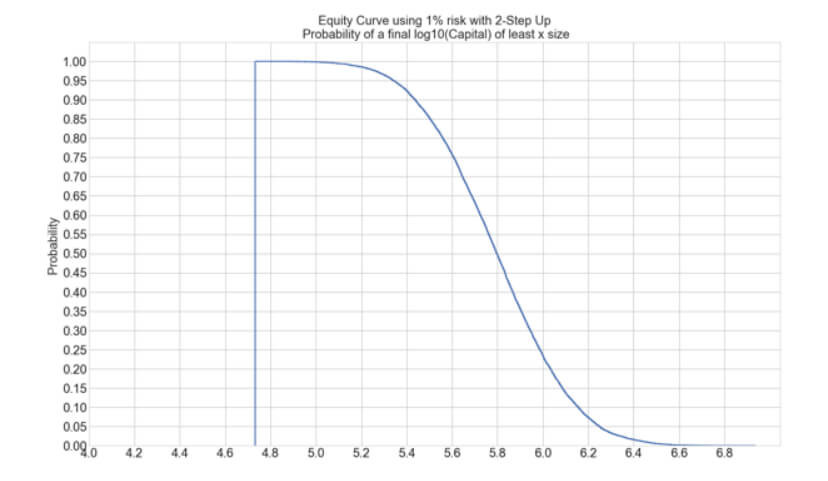
2-Step Up Return Stats:
Average ending Capital: 625,846.08
Max ending Capital : 8,601,130.02
Min ending Capital: 53,941.54
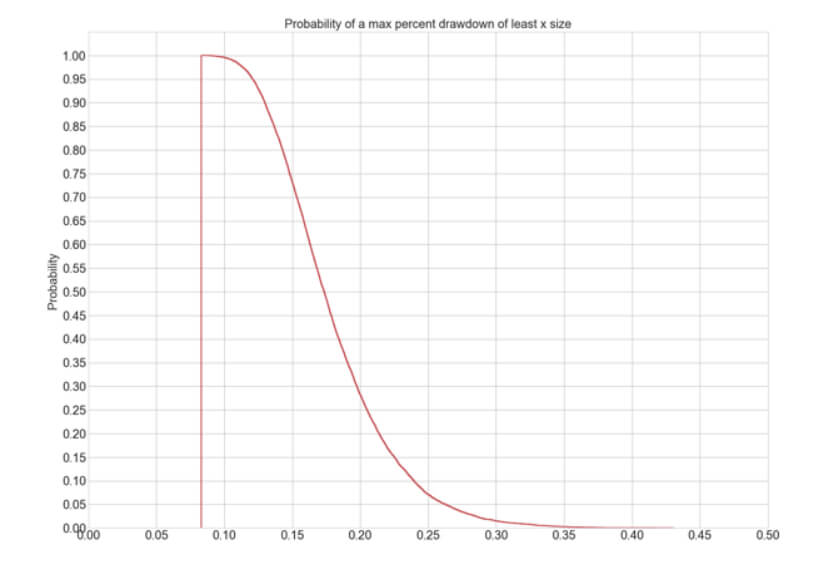
2-Step Up Drawdown figures:
Average Max Drawdown: 18.02 %
Maximum Max Drawdown: 43.04 %
Min Max Drawdown: 8.31 %
Probability of a 10% drawdown: 99.59%
Probability of a 20& drawdown: 28.29%
Probability of a 30% drawdown: 0.03%
3-Step Up Return Stats:
Average ending Capital : 1,597,715.25
Max ending Capital : 34,224,341.81
Min ending Capital: 53,439.67
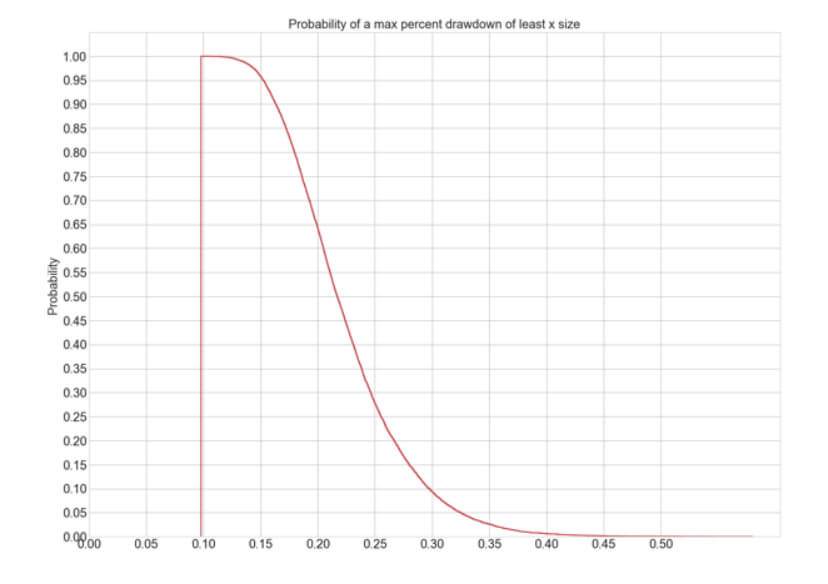
3-Step Up Drawdown figures:
Average Max Drawdown: 22.52 %
Maximum Max Drawdown: 58.01 %
Min Max Drawdown: 9.79 %
Probability of a 10% drawdown: 99.99%
Probability of a 20& drawdown: 64.23%
Probability of a 30% drawdown: 0.63%
A variation of this strategy could be made by re-investing only 50% of the profits. This method will significantly lower the returns, although it will also smooth the equity curve. As an example, let’s see the reward and risk figures of a 3-Step Up with 50% reinvestment:
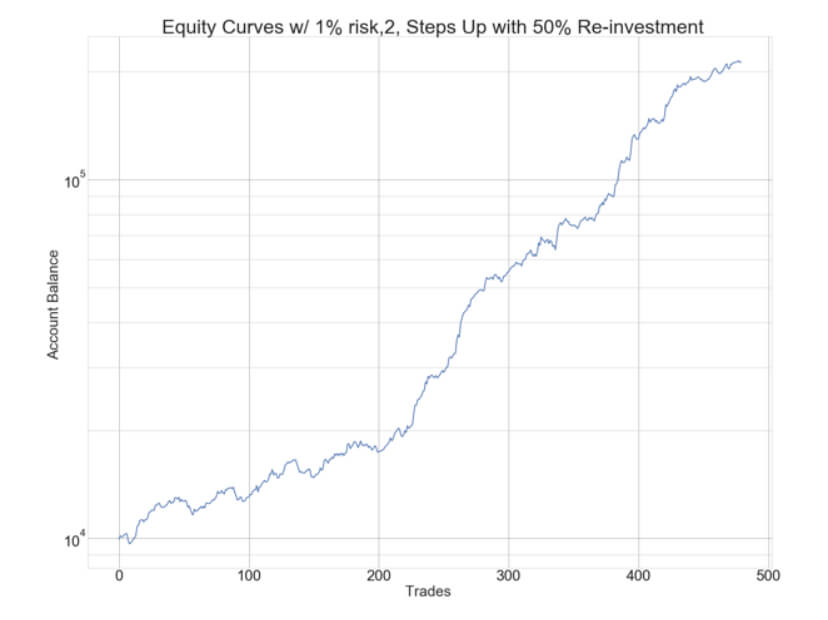
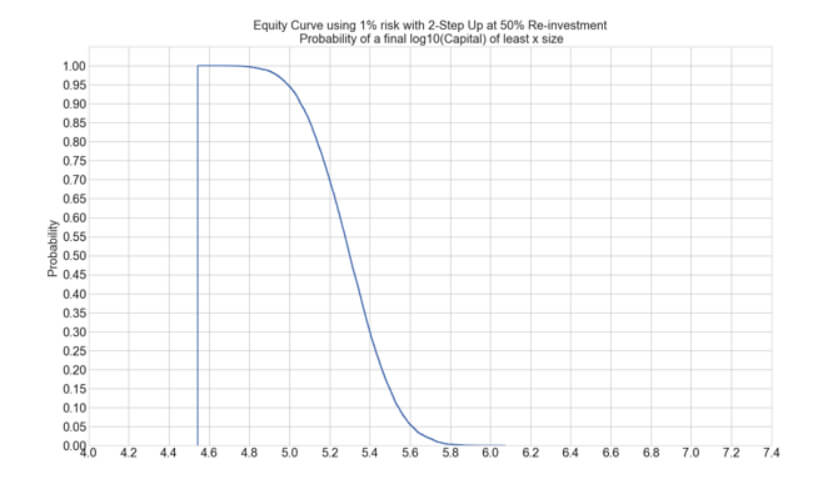
Average ending Capital: 199,952.02
Max ending Capital : 1,181,977.34
Min ending Capital: 34,950.58
Drawdown:
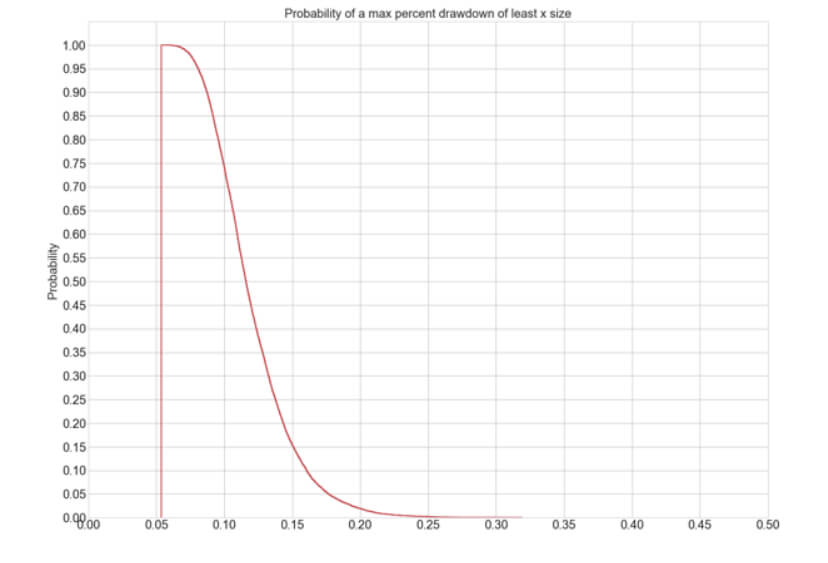
Average Max Drawdown: 12.10 %
Maximum Max Drawdown: 31.89 %
Min Max Drawdown: 5.37 %
Probability of a 10% drawdown: 74.30%
Probability of a 20& drawdown: 1.94%
Probability of a 30% drawdown: 0.00%
We can see that this method is quite similar in performance and drawdown to the 1-Step Up with 100% re-investment, but is not worthwhile, since it reduces the returns to half, while drawdown is only lowered from 13.29% to 12.1%.
Conclusions
We can see that even 1-Step up improves substantially the performance of a strategy (about 4X) with only an increase in the drawdown from 8.% to 13.3%.
We can see also that the best choice for this strategy is 2-Step Up, with a balanced mix returns (average ending equity of $625,846 over an average Max Drawdown of 18%); this is a 10X improvement from the basic 1% sizing strategy with only about 2.2X of drawdown. But, aggressive traders may choose the 3-Step Up strategy, which doubles the 2-Step Up model’s returns with an increase in drawdown from 18% to just 22.5% ( a 25% increment).