Position Sizing VI: The Kelly Criterion
The Kelly Criterion is a formula that finds the optimal amount to bet based on the percent of winners and the reward/risk ratio. It was published by the Texan-born scientist John L. Kelly, in a paper entitled “A New Interpretation of Information Rate.” The formula is as follows:
f% = P – [(1-P)/R]
were, P is the probability of winning, and R is the reward/risk ratio.
For instance, in a coin toss game in which you win $2 when heads and lose $1 when tails,
f% = 0.5 -[(1-0.5)/2] = 0.5 -0.25 = 0.25%
The formula indicates that you need to bet 25% of the available cash for optimal growth.
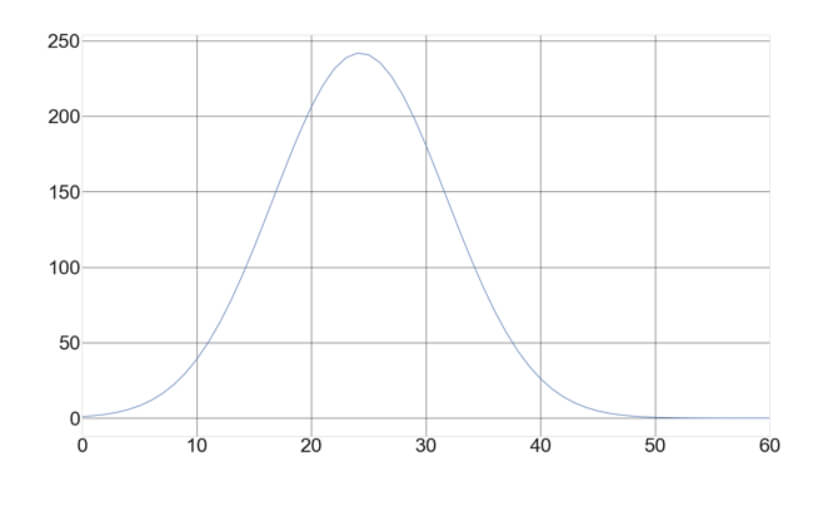
Fig 1 – Final equity as a function of the percent bet. Coin-toss game with a 2/1 profit factor after 100 bets, starting with $1.
The fig 1 shows that in a winning game, there is an optimal bet which allows for the maximal growth of the capital. We can see also that after the optimal bet value is surpassed, the risk increases while returns decrease. Therefore, betting beyond optimal is harmful.
Another interesting fact is that the growth curve is steeper as the number of bets (trades) grows, and decreasing the position size by small amounts will significantly harm the overall growth.
The virtues of trading using the Kelly Criterion
Trading using the Kelly Criterion produces the fastest growth. As an example, the next image shows the progression of the equity curve with the same sequence of gains and losses, using 15% and 25% trade sizes in the mentioned coin-toss game. Please, remember, the game started with 1 dollar, so the figure shown in vertical axis of the image is a multiplier. If you’ve started with $1,000 at the end of the 100 tosses, you’ll end with $30 million using the Kelly Criterion (amber curve).
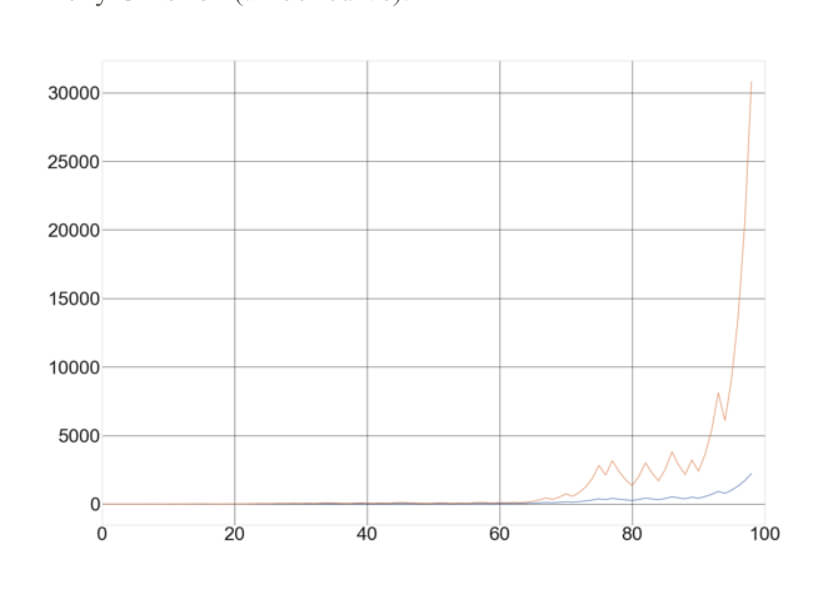
In the image, we can see that the 25% trade had a 30,000X profit in 100 bets, whereas the 15% trade size has a mere 2,200X. That difference grows with the number of bets. We can see also that the difference is not that much in the first sixty trades, but it explodes after trade nr. 70 and especially after trade nr. 90. Thus, the Kelly Criterion does not show its effects in the short-term; thus, trader should let it go long-term.
The downside of the Kelly Criterion
One downside of using the Kelly Criterion is that even on a fair coin-toss game with 2:1 reward/risk ratio in which we know the exact optimal position size (25%), the random nature of the coin toss would make it seem as if the optimal size should be different. The following figure shows 20 different coin toss curves of 100 bets using real random sequences.
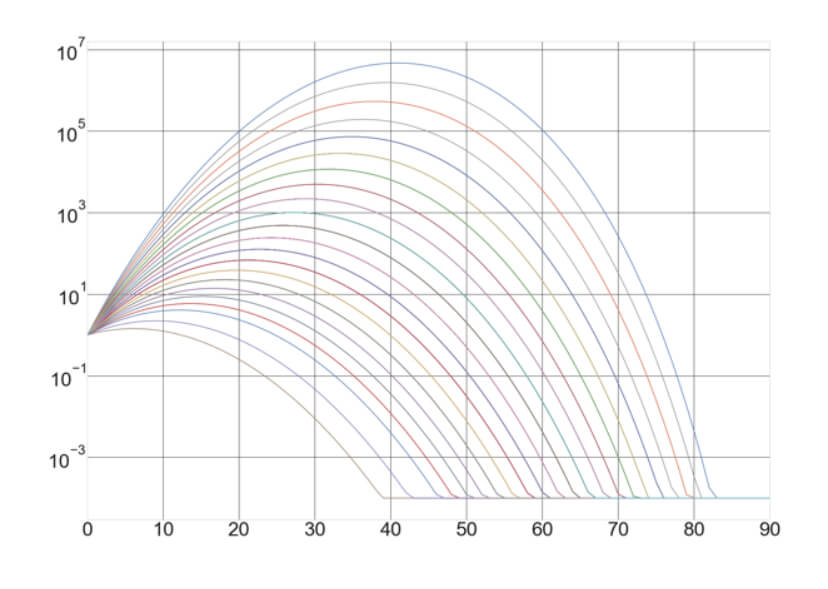
The figure is set to log scale because the difference in the outcomes are so high that a linear scale does not reveal what we are looking for. In the image, we can see that the lower curves show its peak below the theoretical 25, while the more successful outcomes show optimal fractions of up to 42. This explains how difficult it is to find the optimal fraction on a trading system in which we only know the historic parameters, not the true parameters.
Linked to this, comes what we already have said: using the optimal fraction sizes may result in huge drawdowns.
Drawdowns
Similar to the growth curves shown, drawdowns cannot be fully predicted but using Monte Carlo simulations, we can create a good approximation of the typical and maximum values. On the next figure, plotting the histogram of max drawdowns, we can see that the typical value for the Kelly Criterion sizing is about 85% drawdown.
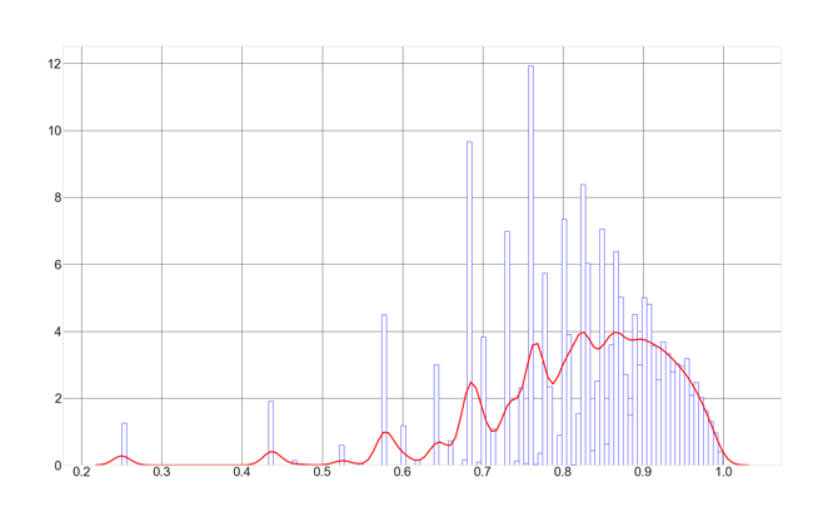
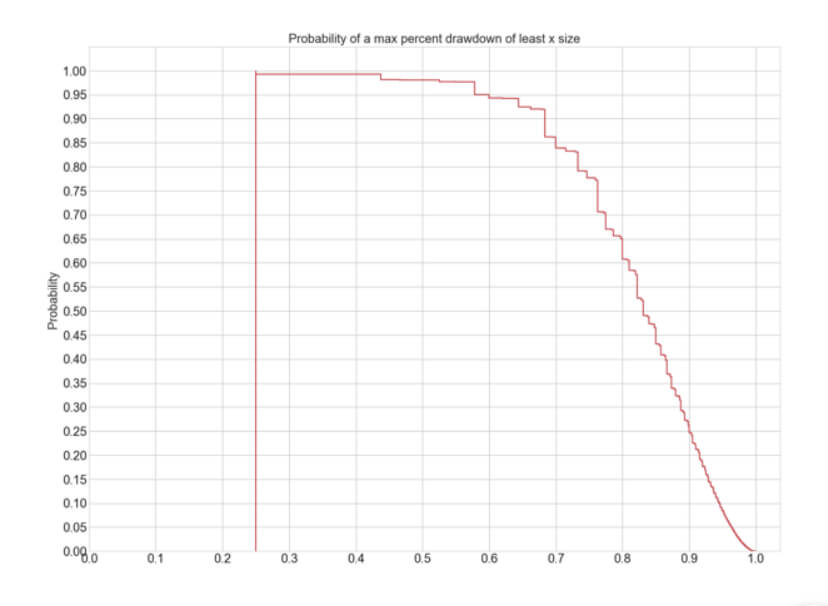
In the next figure, we can see the max drawdown probability plot. We observe that the likelihood of a max drawdown of at least 95% is about five percent in sequences of 100 bets, or once every 20 occasions. Therefore, we should assume the possibility of it happening over time is a sure thing.
So, if the Method is not tradeable, why waste our time?
Although it is rather hard to trade using optimal fractions, we can make use of the concept of maximal equity growth. So, stay tuned for practical applications of the Kelly Criterion in the future.






