That is one key issue when trading. Should I stick with the same trade size, or is it better to compute trade size based on the account balance?
In his book “The mathematics of money management, Ralf Vince answers that question simply and elegantly, so let’s follow Ralph’s steps to dissect this topic.
No Easy Answer
The question of reinvestment or not can’t be answered directly. Let’s see an example where a wining system becomes a loser by reinvest.
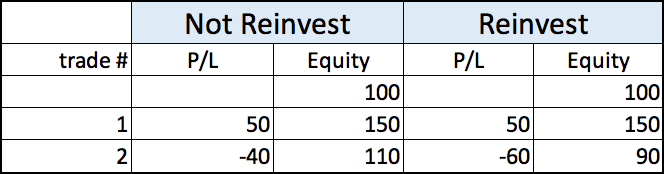
Table 1 – System A
In System A, we have two trades. In the first trade making 50% and -40% in the second one, for a total profit of 10%. If we take the same sequence and reinvest, the system loses 10%.
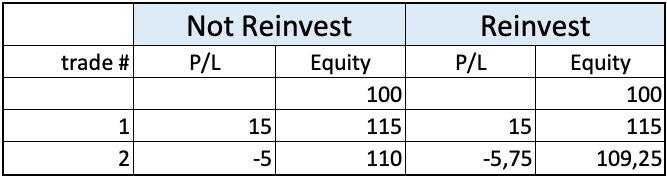
Table 2 – System B
Using System B, we see there is a gain of 15%, followed by a loss of 5% for a total of 10% gain. This system also nets 10% without reinvestment, but it continues being a winner with reinvestment.
Changing the order of the sequence does not alter the final result, provided none of the trades leads the account to a broke (because then the second trade would not be happening). You can make your own calculations, but multiplication is commutative, isn’t it?:
A*(1 +0.15)* (1 -0.05) = A*(1 -0.05)*(1 +0.15)
Geometrical Mean: Key to Qualify Systems under Reinvestment
Let’s add two one-point winners to system A, and two one-point losers to system B.
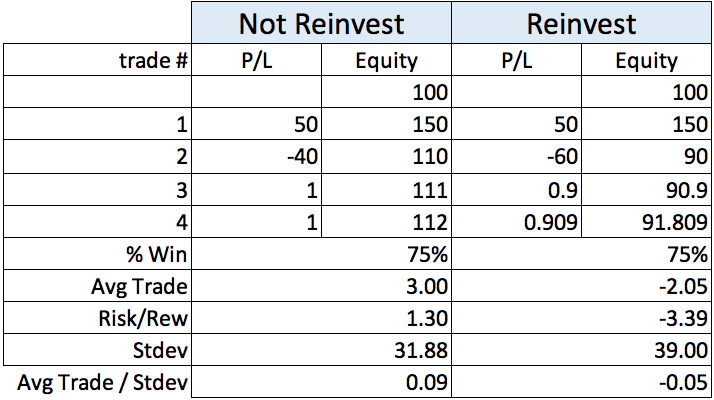
Table 3 – System A
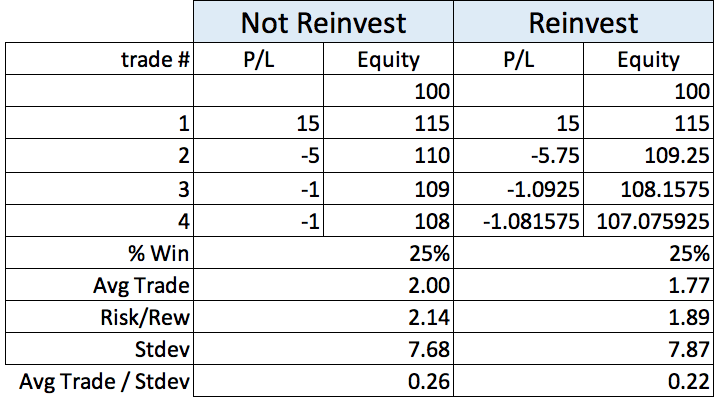
Table 4 – System B
Now we will take as a reference a typical bank account paying one point per period.
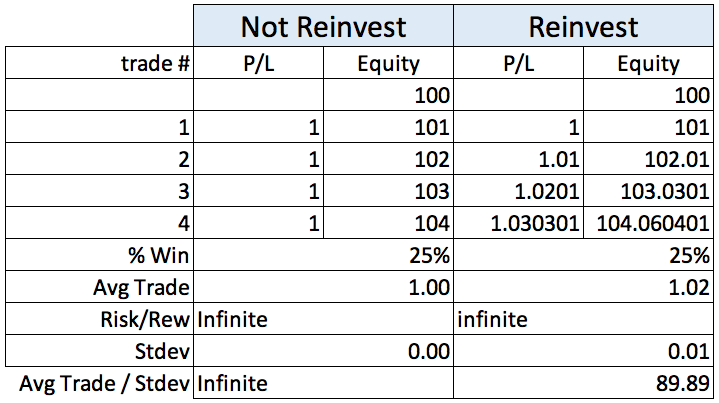
Table 5 – System C
We already know that system B is the optimal one for reinvesting, but, let’s see which parameter defines the optimal system to fulfill our objective to maximize profits under reinvestment. How could we determine which system is the best for reinvesting, given we had only the information of its non-reinvesting performance?
By percentage of winners, system C will be the winner, by average trade or by total dollars the winner is system A. Risk/reward or lowest drawdown is not the answer. If that was the answer, then we should move our money to a bank account.
We know system B has the right mix of profitability and consistency, and systems A and C lack one of these properties. So how to measure this mix?
According to Vince, the right formula is the Geometric Mean, which is the Nth root of what he calls “Terminal Wealth Relative” (TWR), where N is the number of trades. TWR is the cumulative amount we would obtain if the initial amount of the trading account were 1 instead of 100.
TWR = (1+%R1)*(1+%R2)*… (1+%RN)
Where %Ri is the percent returns on each trade.
A simpler formula to express TWR is:
TWR = Final Capital / Starting Capital
And these are the TWR of our systems :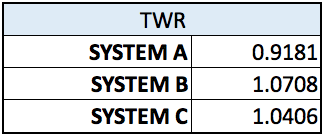
Table 6 – TWR
By taking the square roof of the N trades we obtain
Geometric Mean (G) = TWR^(1/N)
G = (Final Cap/Starting Cap)^(1/Nr of trades)
Let’s see the G of our sample systems
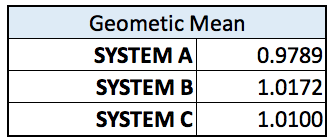Table 7 – Geometric Mean
From table 7 we can see that the best performer in terms of geometric Mean is System B.
Final words
The Geometric Mean is the growth factor per trade. A system with the highest G is the system that makes the most profit and grows the fastest on a reinvestment basis.
A G less than one means the system is not profitable and would lose money when using reinvestment.
If we obtain a G = 0, it means we went broke because anything multiplied by zero is still zero, and G is a multiplicative function. Any big losing trade will have a powerful effect in G. That is a mathematical way of saying, “cut your losses short.”
As Ralf Vince put it: “in trading, you are only as smart as your dumbest mistake.“
Reference: The Mathematics of Money Management, Chapter 1.
The examples of this article were taken from Ralph Vince’s book, although the formulas were checked and computed using an Excel spreadsheet.
