Forex Options III – Option Pricing
Supply and demand

The price of a given option is determined in the real market by supply and demand. That means a buyer and a seller must agree on a determined price to complete a transaction. A buyer willing to buy at market price must pay the ask price. A seller wanting to sell at market price should accept the bid price. Options spreads are usually larger than spot spreads. For instance, the typical spread of a EURUSD spread is 3-4 pips, but its lower risk at a reduced cost makes them attractive to knowledgeable option traders.
A probability game

Options trading is a probability game. The long-term profitability of an options strategy is linked to the traders trying to buy undervalued options and sell overvalued options. Therefore, the trader should have a clear understanding of theoretical versus market valuations, and, in the case of FX Options, knowing the underlying market fundamentals.
The majority of options traders use an option as if it was the underlying, buying calls when they think the asset will go up and buying puts when considering it will go downward. The issue is that options are wasting assets, thus in most cases, that approach is unprofitable.
Structured approach

Most authors consider that to trade options successfully, a structured approach is necessary. A trading plan is needed, and, in addition, developing the discipline to follow it.
The benefits of a structured approach are:
Emotions are eliminated in the decision-making process
There is no psychological need to be right
The best thinking effort is made before the battle, avoiding subjective decisions
The Theoretical Pricing Model
Options are complex investment products as it involves estimating the odds the price of an underlying asset to surpass the strike price within a given time lapse. The most used model is The Black-Scholes equation that uses the price, volatility, time, and interest rates to compute an option’s fair price. The basic idea of the Black-Scholes model is that the right to delay a decision ( to buy an asset at a specific price) has a value, which can be computed.
A general trait of these models is the assumption that the distribution of prices in the market is Gaussian or something close to it, on a logarithmic scale. Although the Gaussian distribution is an approximation to the way prices move, it is essential to understanding the pricing model’s statistical nature.
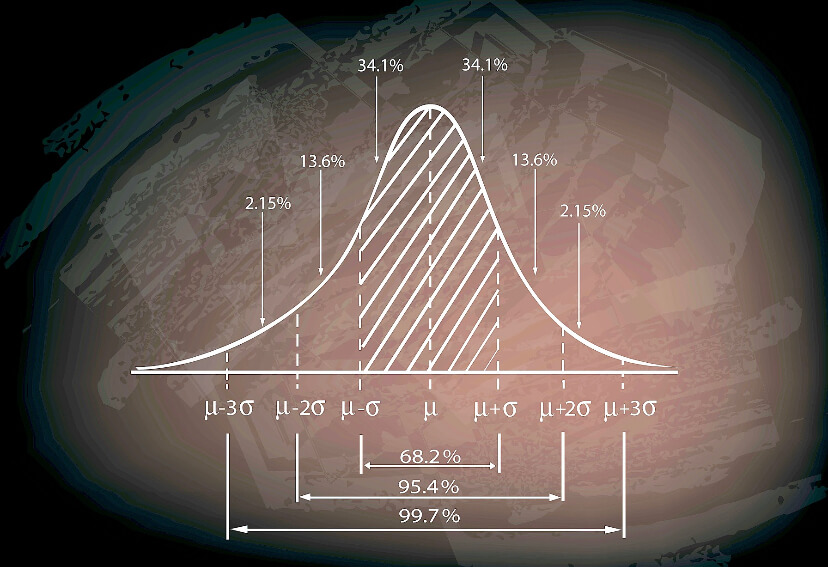
Under this model, the price movements of the underlying assets move also following the Normal Distribution. If you’ve followed us in our Stats for traders” video series, you’d understand by now that 68,2% of the values following the bell-shaped curve lie within one standard deviation (SD) from the mean and 95.4% of them lie within two SDs.
That means only 31.8% lie away more than one SD, and just 4.6% go farther than two SDs. In the case of an option, we are interested in only one side of the bell curve. In this context, only 15.9% of the data points lie beyond 1 SD, and 2.3% beyond two SDs.
The Black-Scholes-Merton Formula
C(S0,t) = S0N(d1) -Ke-r(T-t) N(d2)
S0N(d1): The Intrinsic value
-Ke-r(T-t)N(d2): The time value of the option
d1 and d2 are calculations of the area of a point in the curve, which will show the price’s odds to reach that point.
As said, the Black-Scholes-Merton equation assumes that price movements follow the Gaussian Distribution. That, combined with an expiring date and the knowledge of the volatility (sigma) of the asset, are the key ingredients to assess the fair price of the option.
If we were to buy at the absolutely fair price, the model would predict zero gains and zero losses in the long term. But the volatility in the market is not constant but changing. Therefore, the ability to evaluate which options are cheap or expensive, under our forecasted scenario showing a higher (or lower) future volatility is one of the elements for success.
In the next video of this series, we will develop the volatility concept applied to options.
Recommended reading:
THE OPTION TRADER’S GUIDE TO PROBABILITY, VOLATILITY, AND TIMING , by Jay Kaeppel






