Basic Probability Concepts II
In this video, we will continue to uncover the basic ideas about probability and the rules of summation and multiplication.
Probability
Probability is the term given for the measure of the likelihood of an event to occur. If we are entirely certain that the event will occur, the probability is one, or 100 percent. If an event can’t occur, the probability is zero. If the event is equally likely to occur or not, its probability is 0.5 or 50%. Thus, we see that the probability ranges between zero and one. No probability can be greater than one or less than zero.
Estimated probability
Usually, In science (and trading), there is no way to know the probability value in advance. In this case, the usual way to assess it is to do a finite number of trials and calculate the relative frequency of occurrence or the proportion of the event. This value is not the real probability, but an estimate of the probability. The larger the number of trials, the more accurate this estimate is.
The concept of estimated probability is really important because a lot of people think that the probability obtained using a sample is the real one when, in fact, it might be too optimistic or pessimistic. That is, the sample, by pure luck, can bee too good or too bad.
There are other cases, for example, the roulette, the roll of a die, or a fair coin toss, where the probability of occurrence is known in advance. In that case, it is quite easy to compute it.
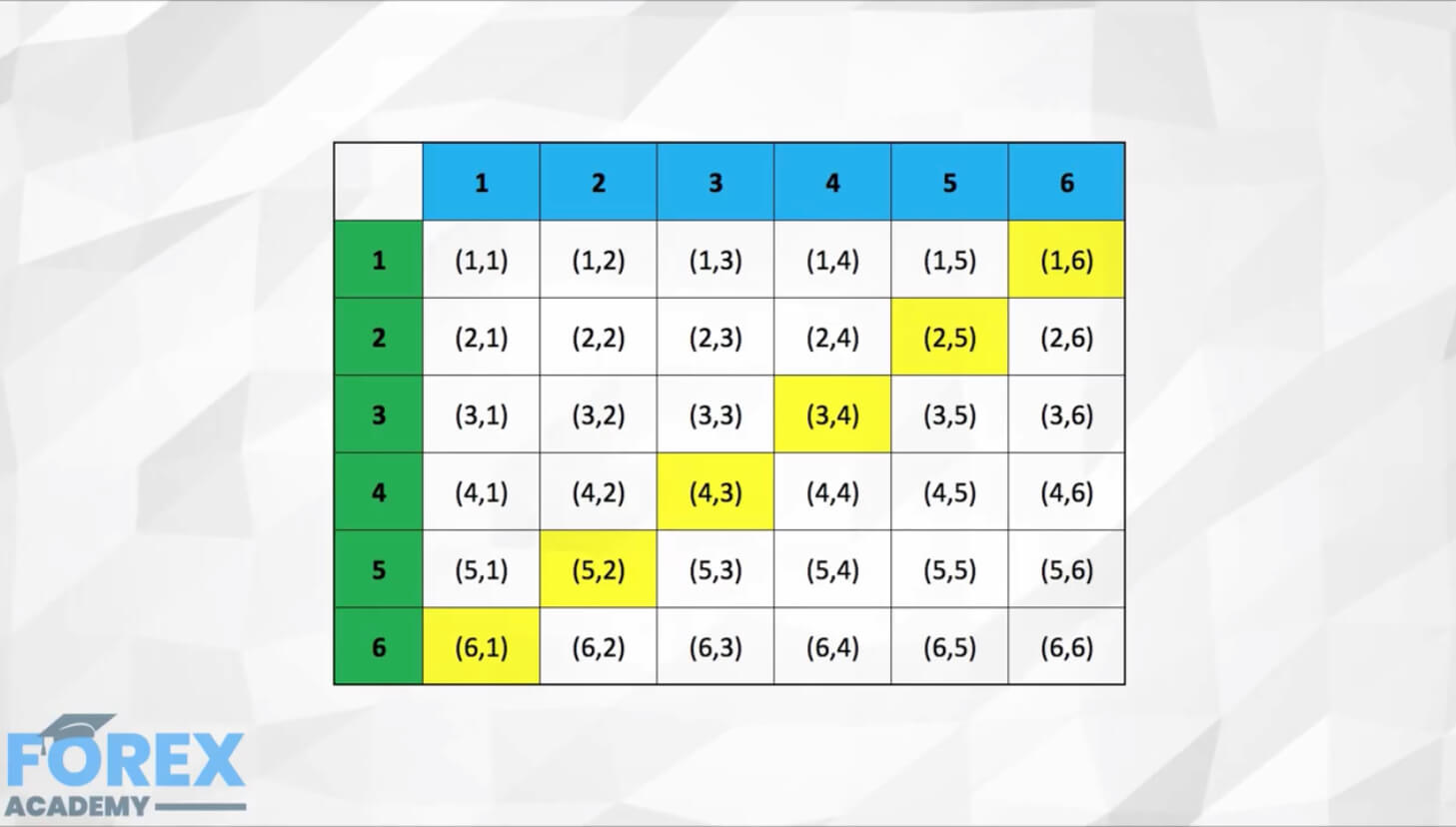
The probability of an event happening is the number of ways that event can occur divided by the total number of cases. For example, the probability of obtaining a one in a die rolling is one divided by six, or 1/6. The probability of a seven to occur in a two dice rolling is six occurrences out of a total of 36 combinations. Thus one in six. The probability of a two-coin toss obtaining one head and one tail is two possible cases divided by four total combinations of head and tail, thus, 0.5 or 50%.
Fair odds
Fair odds is another quantity which gives information about the probability and comes from gambling. If a game is to be fair, each player should expect no advantage, no edge. Then, if the likelihood of the possible outcomes is different, the amounts to bet should be modified to compensate for this fact.
Let’s say the probability of one result is 2/3, then the probability of failure is 1 – 2/3 = 1/3. Thus, to make the game fair, for every dollar rewarded on the success, two dollars should be paid on the failure.
In general if P_success = p, then P_failure = 1-p, and the odds in favor are
p/(1-p) to 1.
Also, the odds against success are
(1-p)/p to 1.
Rules when Combining Probabilities
Addition Rule
Adding probabilities mean answering the OR question, such as “what are the odds of event A or B or C happening.”
For the addition rule, we have two cases.
Mutually exclusive events
With mutually exclusive events there is no overlap. If one event happens, the other events cannot occur. In this case, the probability of occurrence of A, or B, or C is the sum of the probabilities of each.
For example, what are the odds of getting an even number on a rolling die?
We know that there are three even numbers in a die: two, four, and six, each having 1/6th probability of occurrence. Thus the likelihood of getting an even number is 3 times 1/6 or 0.5.
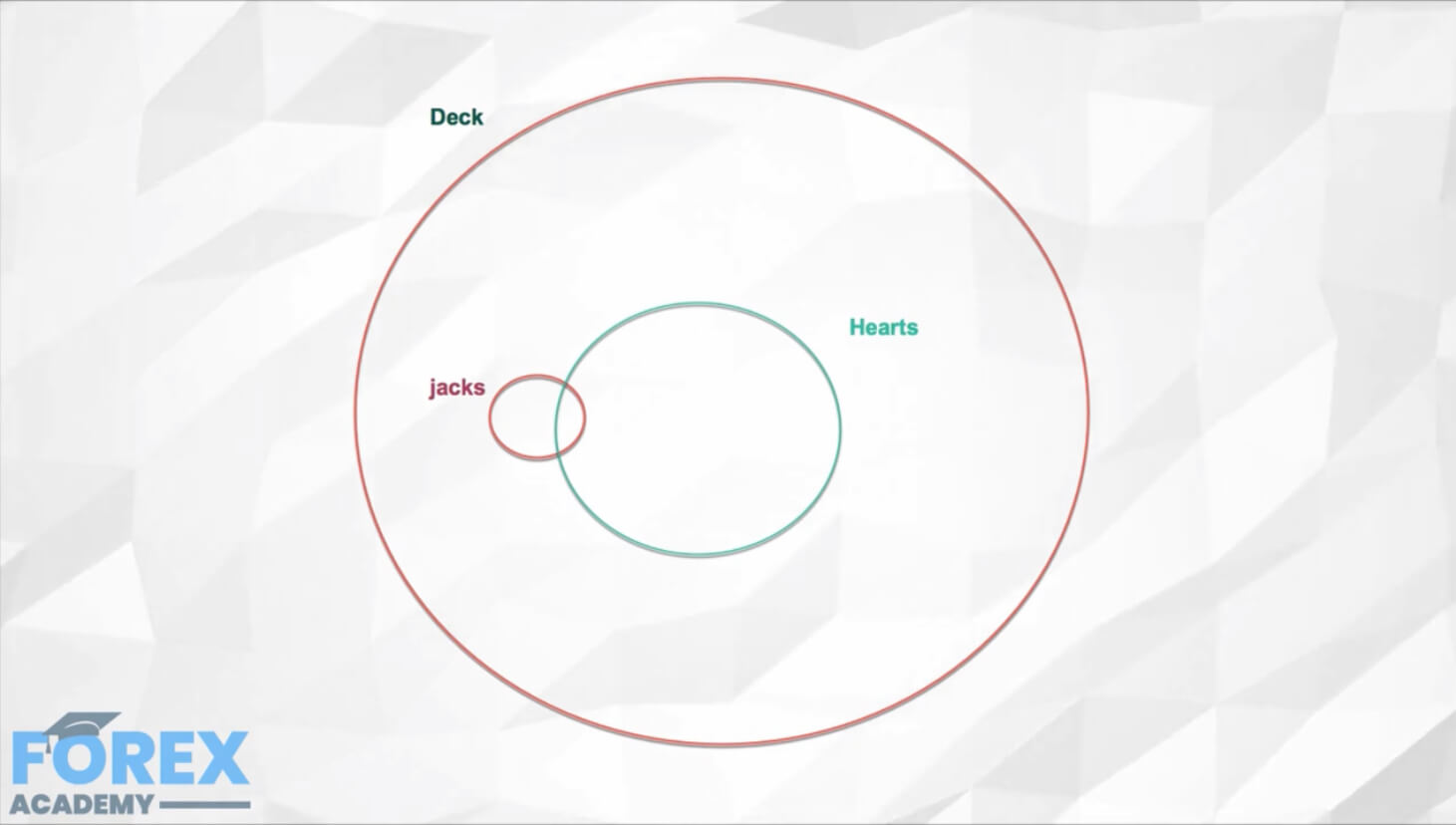
Non-mutually exclusive events
If the events are not mutually exclusive, there can be overlap between them. This can be visualized in a Venn diagram. In that case, the probability of the overlap must be subtracted from the sum of separate events.
For Example, If one card is drawn from a 52-card deck, what is the likelihood the card is a Jack or Heart?
P_Jack = 4/52
P_Heart = 13/52
P_[Jack and heart] = 1/52
Then the answer is:
4/52 +13/52 – 1/52 = 16/52
The multiplication Rule
Multiplying probabilities answer the AND question, such as “what is the probability of A and B happening?
If the events are independent, then the occurrence of one event does not affect the appearance of the others. in this case, the odds of several events happening together is the product of their probabilities.
For example, what are the odds in a coin toss game of having two heads in a row?
We know the odds of each head is 0.5, then the odds of having two heads in a row is 0.5×0.5 = 0.25 or 25%.

To know the odds of an N losing streak of a trading strategy is rather easy: We just need to know the percent losers of a system, which is 1- Percent_winners, and multiply it by itself N times ( which is the exponential operator).
For example, which are the odds of obtaining eight losers in a row if the percent winners of my strategy are 45%?
Answer: If P_win = 0.45, then P_loss = 0.55.
P_8_Drawdown = 0.55^8 = 0.84%
If the events are not independent, we should use the conditional probability formula, but this is an advanced subject beyond the scope of this video.