Novice traders put their focus on how much leverage brokers are offering as a crucial part of their decision process to choose the right brokerage account. But in fact, as we saw in our previous article, Things you should Know about Leverage, Drawdown and Risk , there is no need for leverages above 30X, and in 99% of the cases, leverage is the rope with which traders hang themselves.
In this article, we will show that compounding is a terrific tool to boost the growth of a trading account.
In our article To Reinvest or Not Reinvest, That is the Question, we discussed the properties needed for a trading system to be suitable for reinvestment strategies.
Unhappily, 95% of the traders fail. The main reason for failure is discovered in the final section of the article. The article unveils that the growth factor of any investment strategy is called the Geometric Mean (G).
The Geometrical Mean G = TWR^(1/N) has two operators.
N the number of trades registered on the system, so it is just a normalization factor to equate all systems no matter how many trades were recorded.
Thus, TWR is the key. TWR means Total Wealth Return and is
TWR = SUM(1+%Ri)
where %Ri is the individual percent gains and losses.
TWR is a product of (1 + the individual gains). If the gain is negative (a loss), this particular factor will decrease the total value of the account by the percent that was lost. If the gain is positive, it will increment it by the percent gained.
As an example, let’s say that 1,000 USD is the initial amount in a trading account, and two trades were performed. One lost 10%, and the other gained 15%. Which is the final TWR of this account, and which is the final balance?
TWR = (1- 0.1)*(1+0.15) = 0.9 *1.15 = 1.035
Final balance = TWR * Initial Capital
Final Balance = 1.035 * 1,000 = 1,035 USD
In this simple example, we clearly see that a system with large losses greatly hurts the growth of the investment.
For instance, if the first loss were 50% then
TWR = (1-0.5) * (1+0.15) = 0.5*1.15 = 0.575
and Final Balance would be =575 USD
Of course, 100% loss would mean the account wiped out and no second chance to make it grow. Therefore, it seems wise to concentrate on steady and continuous gains and cut losses short. Let’s explore the long-term performance of low-risk position sizing strategies.
It is evident that a loss limit of 1 percent of the trading capital on each trade looks much better than a ten percent loss in our TWR equation. The issue here is how it performs as generator of growth.
As a first approximation of what we could achieve, let’s look at an equity curve that might seem boring. It is the equity curve of a 26% yearly continuous growth. That was the rate of return Berkshire Hathaway gave his shareholders.
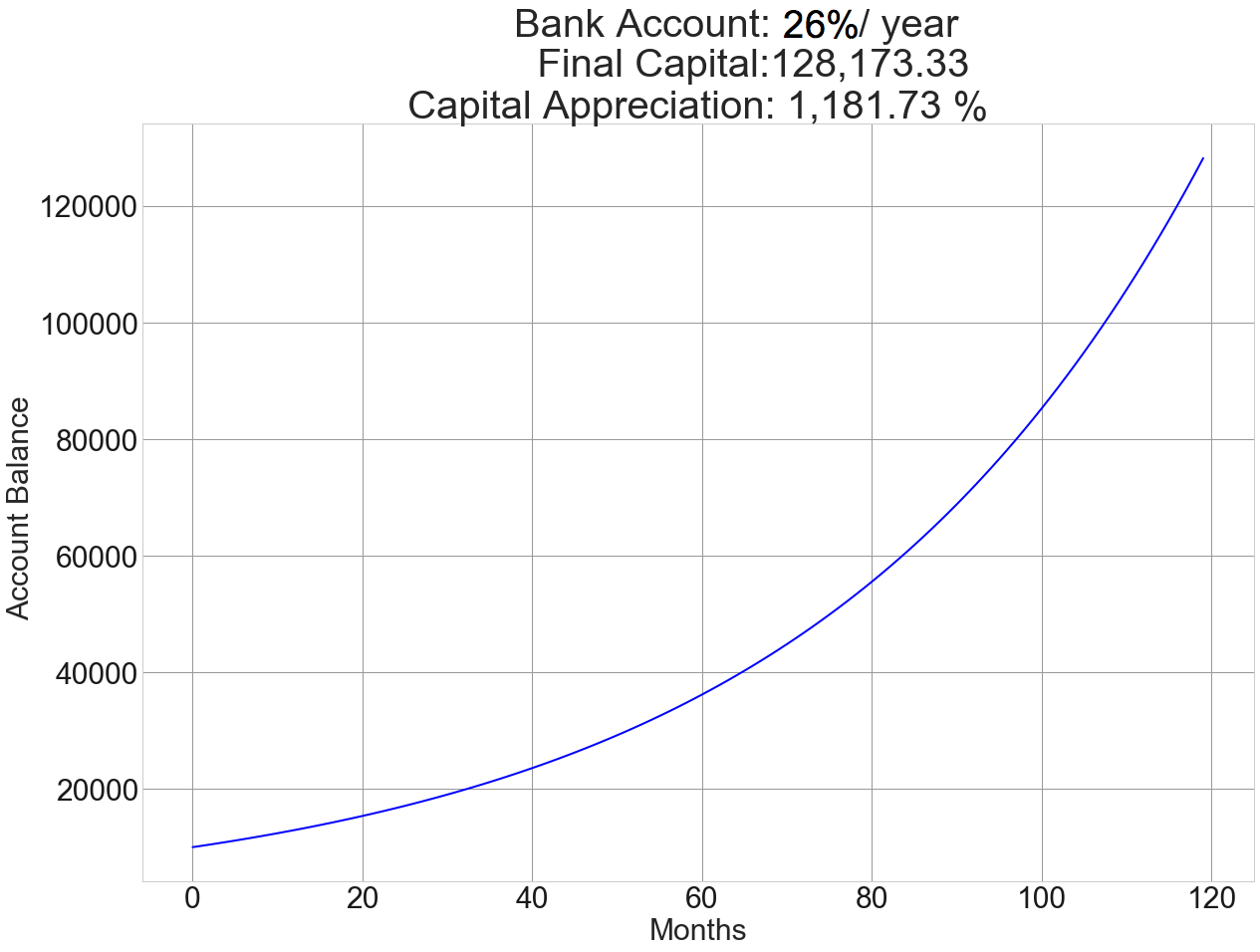
Fig 1 – 10-year chart of risk-free 26%/year returns
In this chart, we show ten years of 26% compounding interest. With an initial balance of $10,000, the final capital is $128,173.33 for a capital appreciation of 1,182%. Not a bad feat!
Well, let’s look at what this strategy does in 40 years:
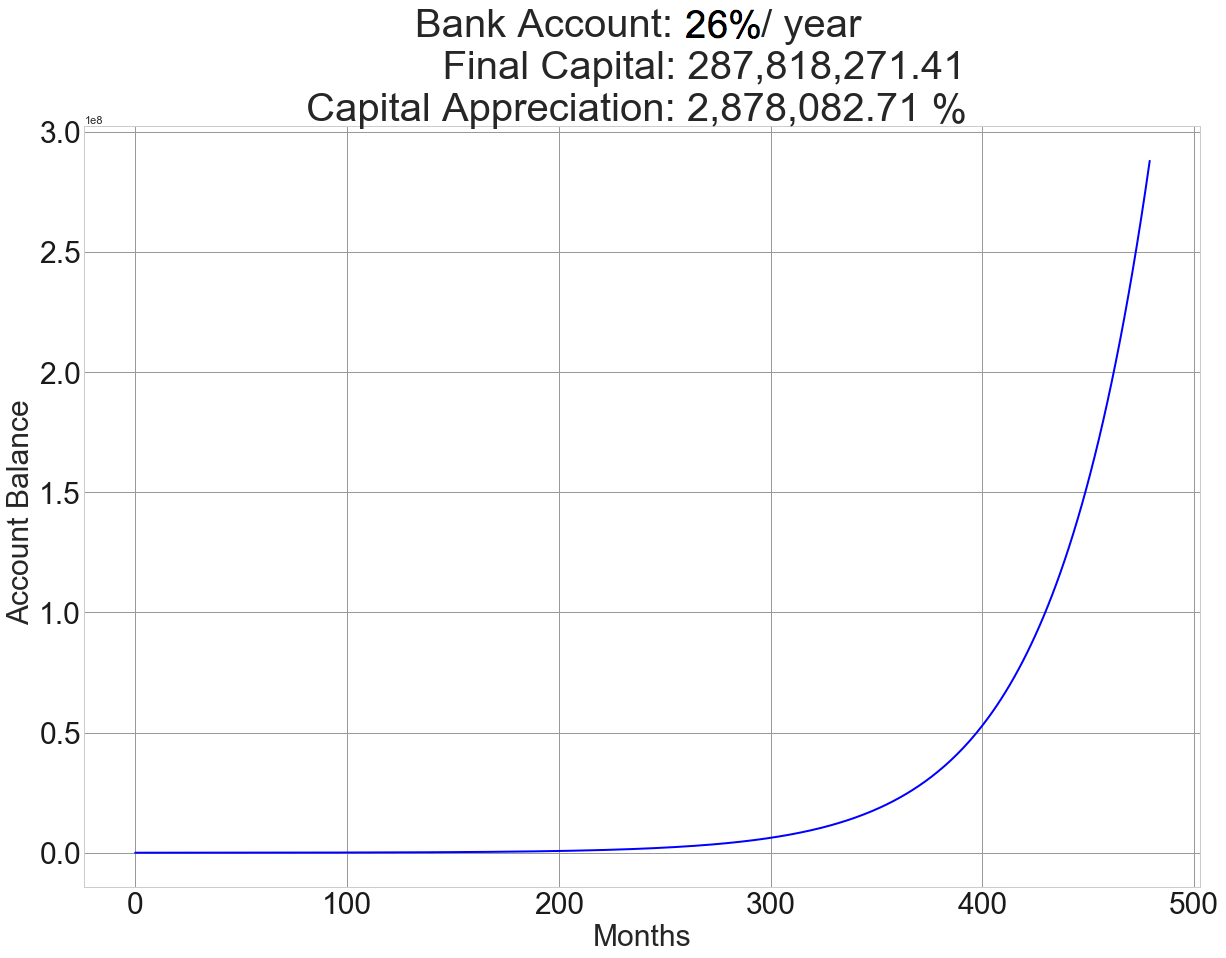
Fig 2 – 40-year chart of a risk-free 26%/year returns
We can see that in 40 years, this strategy converts $10,000 into 287,818 million dollars and a total growth of 1.88 million percent.
I know, waiting forty years is too much for the instant-satisfaction generation. Maybe we don’t need to wait so long. But before going further, let’s see the properties of this curve. On the 10-year graph, we can see that it takes 400 months to reach $500,000 and just 100 more months to go from 0.5 to almost 3 million. Compounding needs patience and perseverance because its power comes from the accumulation of past gains.
A Trade sizing system for the faint-hearted
We are going to use a Forex discretionary system that was used live by a friend. Since we don’t have 40 years of history for it, we will extrapolate it with resampling with replacement to simulate its performance. The system will take three daily trades 20 days per month.
To refresh our memory, the following are the relevant statistical data of the system:
STRATEGY STATISTICAL PARAMETERS : Percent winners : 58.74% Profit Factor : 1.74 mean Reward Ratio : 1.22 Sample Statistics: Mathematical Expectation : 0.0628 Standard dev : 0.4090 Mathematical Expectation using Bootstraping, Samples=100K, confidence limit 99%: Expectation interval low : -0.01 high : 0.1776
The main parameters are 58% winners and an average reward to risk ratio of 1.22.
The following chart is one year of simulated performance of this system using a 1 percent risk on every trade:
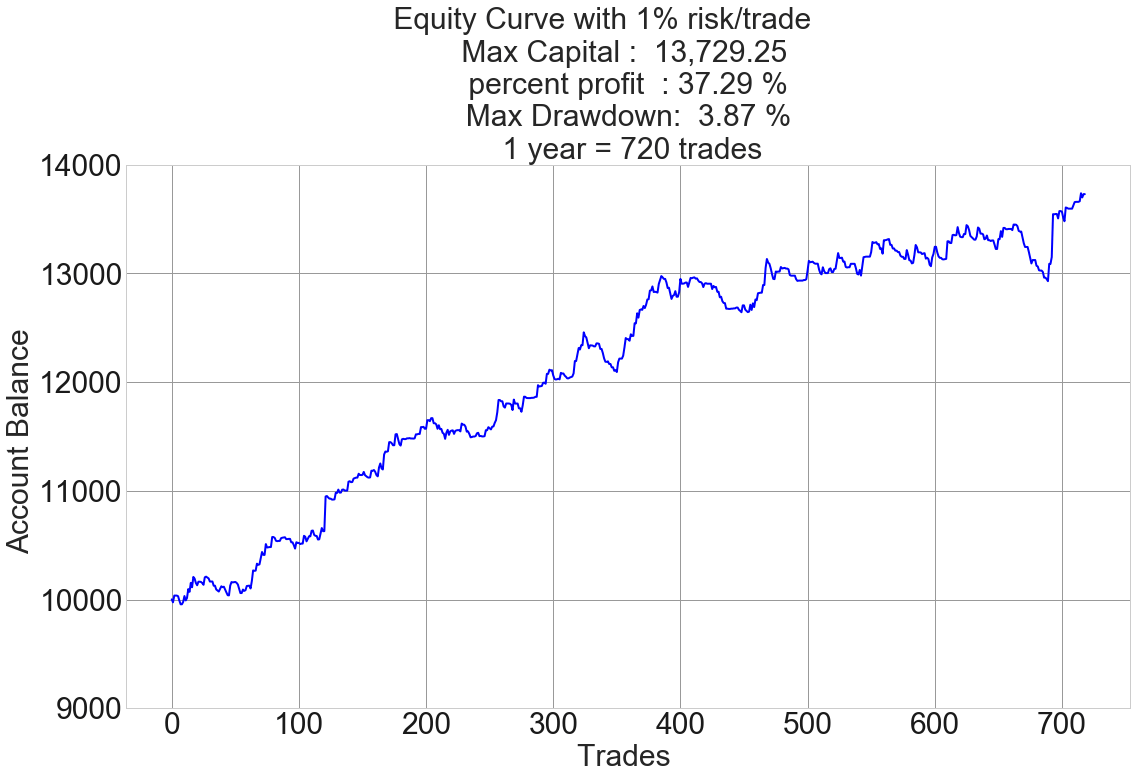
Fig 3 -1-year chart of 1% risk Model Forex System
The figure also shows all the relevant information needed. We see that the system was able to move the initial balance from $10,000 to $13,729.25 for a total profit of 37.29 percent and a max drawdown of just 3.87%. That system beats Berkshire Hathaway Inc, by a fair margin.
Let’s see what it can do in 20 years:
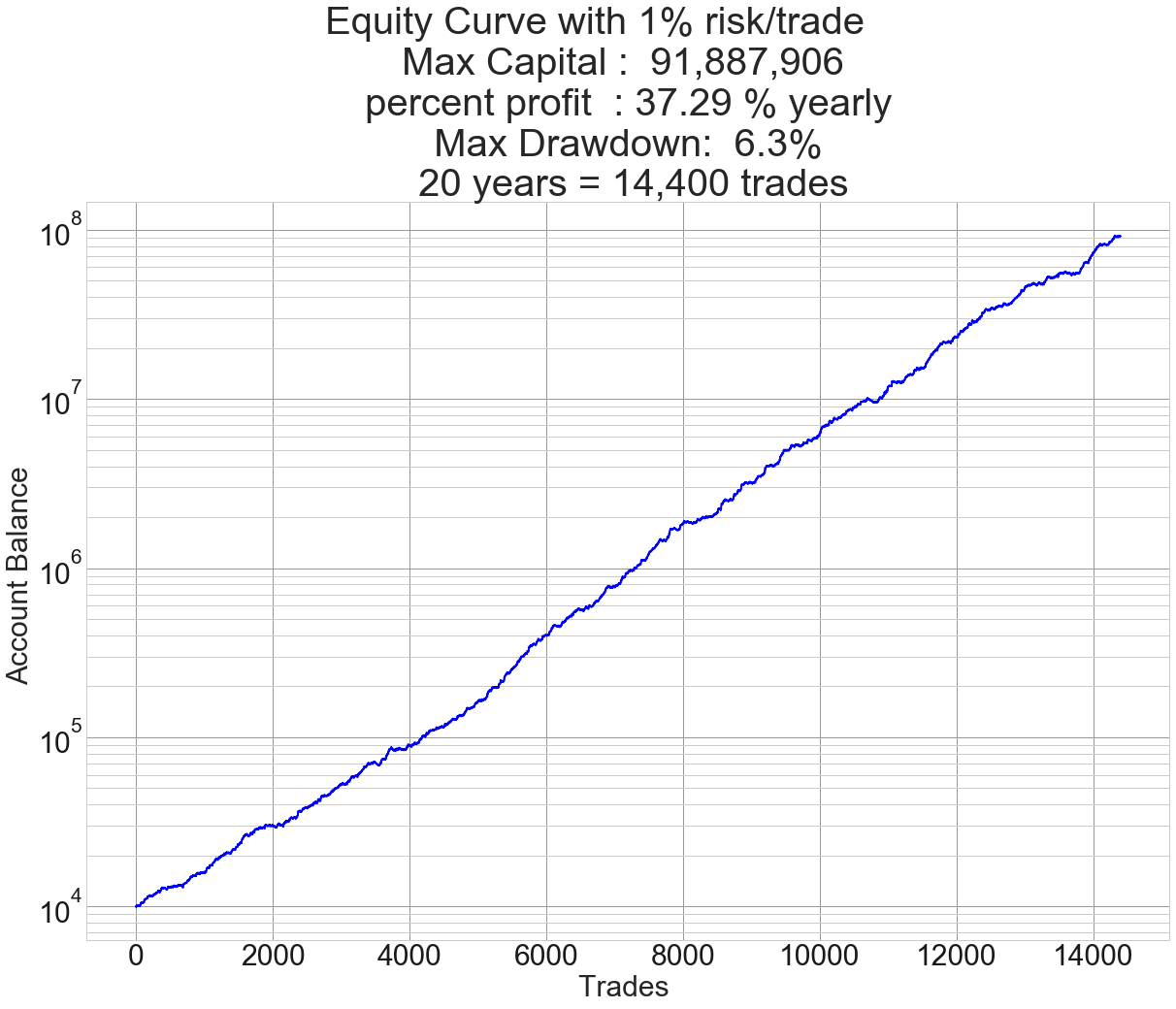
Fig 4 -20-year chart of 1% risk Model Forex System
We can see that this modest system can produce $91.8 million in 20 years with no more than 6.3% drawdown.
We have shown here that there is no need for high leverages and drawdowns to be successful and rich in the long run. But to show you the power of compounding, let’s show here the 20-year equity curve using a 2 percent risk to observe that drawdowns above 20% are not needed at all and that high leverages are totally unnecessary.
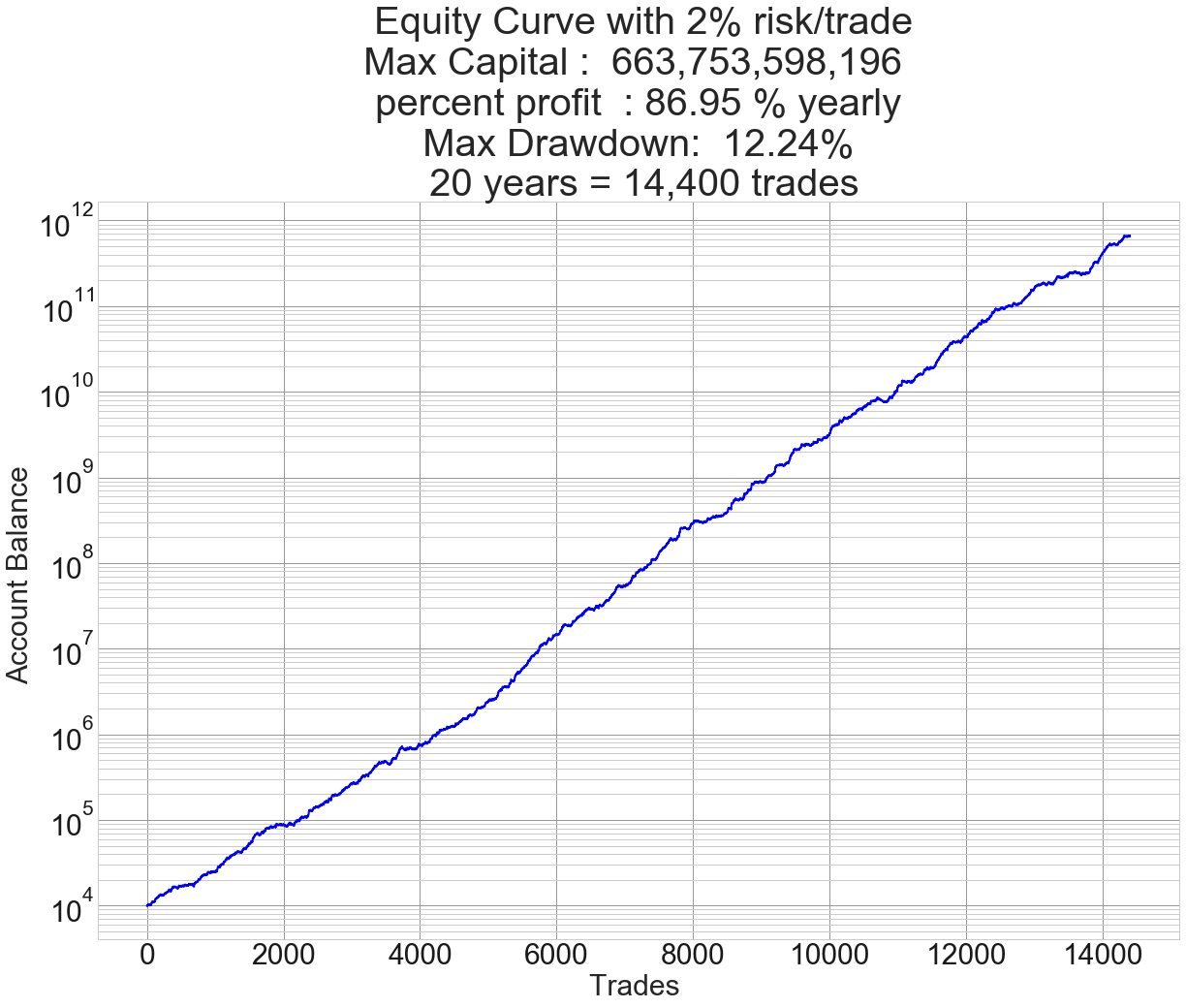
Fig 5 -20-year chart of 2% risk Model Forex System
This system gets the insane amount of $663 billion in 20 years with just a 12% drawdown, and the first 100 million is reached before year 10, starting with only $10,000.
We could go even to 3 percent. I did the numbers, and still, the drawdown is below 20% for insane theoretical profits. Of course, the system would break down well before such amounts could be traded.
The key idea is to show that insane risks are not the way to richness. The way to wealth is compounding with a controlled risk state of mind.






