Most of the people wanting to profit from the Financial Markets think that the secret to success lies in knowing the price turns to start a new trend and also detects when to get out of the trade. They might be right if there were a mathematical formula or crystal ball to show us the right timing. But the truth is the Financial Markets are chaotic and random. Thus, there is no sure way to be right.
The good news is that we don’t need to be right, but be profitable. That can be achieved by taking small losses when the trade goes against us and let profits run when the trade goes as we projected. And the key knowing if we are on the right track is measurements and analysis.
This article deals with how to extract information out of a set of results by computing an average. And also, by measuring the deviation from the norm extract wisdom hidden in the data collection.
Averages
Averages have the purpose of determining the typical value or center of a set. For instance, the mean profit achieved in a month or a year. We assume that the majority of the samples are located near the average, and, also, that the number of cases away from it decreases with the distance to the average.
The computation of an average is simple. We add all elements and divide them by the number of items in the set.
As an exercise, if we have a collection of trading results X, with elements x1 = $1, x2=$-1 and x3=$3 which is our average profit?
Average of X (M) = (x1+x2+x3 )/3 = (1+(-1) +3)/3 = 3/3 = 1 dollar.
The Sample Standard deviation (SD)
It is interesting also to measure how far could we expect the following trades to be away from this mean. There are several ways to measure errors, but the most used is the Standard Deviation. SD for short.
Computing the standard deviation is a bit more complicated than the average, but not much.
1.- We take the difference between the mean and every element, creating a new set of differences.
dxi = M-xi
2.- Differences may be negative or positive, so we square them to get dxi^2, creating a set of squared differences.
dxi2 = dxi^2
3.- We add all elements of this last set and divide by its n-1, the number of items minus one. This result is called variance
Var = Sum(dxi2)/(n-1)
4.- Take the square root of the variance.
SD = √ Var
let’s do it with our example:
1.- dx1 = 1-1 =0; dx2 = 1-(-1) =2; dx3 = 1-3 =-2
2.- dx1^2 = 0; dx2^2 =4; dx3^2 =4
3.- Var = (0+4+4)/(3-1) = 8/2 = 4
4.- SD = √4 = 2
After that, we can conclude that our system’s future performance will be one dollar plus or minus 2 dollars.
The Standard Deviation can be thought of as the average of the dispersion of the results.
Chebyshev’s Inequality
Once getting these results, we know a bit about our trading system. Chebyshev’s inequality gives us another handy piece of information. It addresses the question of how many of our samples will lie within a certain distance from its mean.
There are many classes of probability distributions. One of them is the Normal Distribution, with its typical Gauss or bell curve. The Normal distribution is very nice indeed, and many physical phenomena conform with it, such as the length of people or the distance from the target on a dart game. Unhappily, trading results do not conform to it.
The good news is that the Chebyshev’s inequality works with a wide variety of distributions, and guarantees that no more than a certain fraction of values can be farther away than a certain distance from the mean.
Specifically:
No more than 1/k^2 values can be farther away than k* SD
We can say it the other way around:
At least 1-1/k^2 of the values of a distribution are within k*SD from its mean. If we create a spreadsheet using these formulas we get:
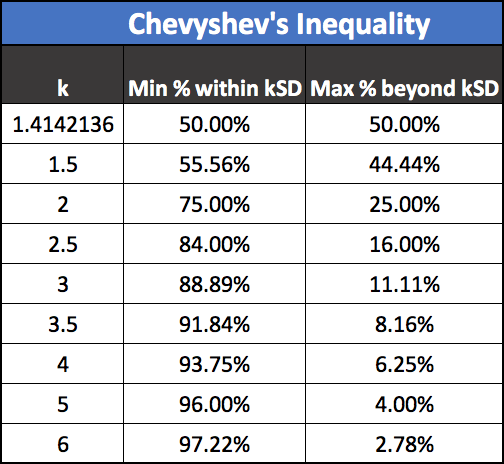
Table 1 – Chebyshev’s Inequality
This table provides a lot of information. We see, for instance, that only 11.11% of the trades are farther than 3 SD from its mean.
- That means close to 90% of the profit on future trades in the above calculation will be between -5 and 7 dollars.
- Also, 75% of them will lie within 2 SD – between -3 and 5 dollars.
Since it can be applied to most of the distributions, we could use it with prices. That way, we could determine how far a price is away of its mean and assess overbought and oversold conditions with statistically relevant tools.
Final words
- Knowing how to compute averages and the standard deviation will help traders quantify and qualify their performance.
- It is interesting to know how to find the odds for a value to be at a determined distance from the mean value of the distribution.